Chcę się pouczyć do kolokwium, ale na zdalnych w ogóle nie mamy materiałów do nauki. Polecicie jakieś źródło do tego typu zadań z rozwiązaniami krok po kroku? A może ktoś chętny, żeby mi to wytłumaczyć za $?
#matematyka #studbaza #korepetycje
#matematyka #studbaza #korepetycje
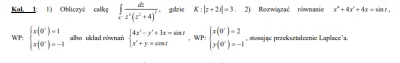
konto usunięte via Wykop Mobilny (Android)
Komentarz usunięty przez autora
Komentarz usunięty przez autora












































#matematyka