Wszystko
Najnowsze
Archiwum
62
Jak zrozumieć paradoks Monty'ego Halla?

Paradoks Monty'ego Halla jest jednym z najbardziej znanych i zarazem bardzo nieintuicyjnym paradoksem rachunku prawdopodobieństwa. W tym filmie postaramy się go zrozumieć.
z- 28
- #
- #
- #
- #
- #
- #

źródło: temp_file5610366969988604052
Pobierz- 0
- 4
14
Anomalie i paradoksy w grach losowych
Ciąg dalszy miniserii o Lotto. Czy wybory graczy są rzeczywiście niezależne? Skąd się biorą anomalie w rodzaju 11 głównych wygranych w jednym losowaniu? Czy ta sama szóstka może być wylosowana dwukrotnie?
z- 2
- #
- #
- #
- #
- #
- #
353
Kombinatoryka, prawdopodobieństwo i Lotto

Jak obliczyć liczbę kombinacji i prawdopodobieństwo ich wystąpienia? Dlaczego czasem nikt nie wygrywa głównej nagrody w losowaniach Lotto, a czasem jest kilkunastu wygrywających? Jaka jest szansa, że te same szóstki mogą się powtórzyć w różnych losowaniach? O podstawach matematycznych gier losowych.
z- 209
- #
- #
- #
- #
- #
- #
- 3
Tylko pomyśl.
---
Daj plusa jeśli pomyślałeś o
- 1
Tylko pomyśl.
---
Daj plusa jeśli pomyślałeś o
- 1
W ciągu 3 lat wydałem 20-25 tysięcy na kupony lotto (dawniej duży lotek).
Czy wobec tego teraz grając dalej mam większą szansę, że nagle wygram, niż gdybym nigdy nie grał?
#lotto #matematyka #prawdopodobienstwo #kiciochpyta
─
Czy wobec tego teraz grając dalej mam większą szansę, że nagle wygram, niż gdybym nigdy nie grał?
@mirko_anonim: nie.
- 1
#s--s #statystyka #prawdopodobienstwo #matematyka
- 1
W mini lotku 27 razy padły te same liczby wygrywające główną wygraną, nie za dużo?
@Hymenajos:
Przeczytaj:
https://pl.wikipedia.org/wiki/Paradoks_dnia_urodzin
Zrozum.
Wtedy nie będą cię dziwić takie "przypadki".
- 2
- 0
Mógłby ktoś mi pomóc, bo zgłupiałem trochę już na pierwszym podpunkcie. Wiem, że omega = 36, ale nie wiem jak zrobić podpunkt a)
Rzucono dwukrotnie kostką do gry.
a) Wyznacz funkcję prawdopodobieństwa sumy wyrzuconych oczek.

źródło: comment_1665673149gOPZKVzZ4YjpnkN4zxo6XO.jpg
PobierzDla was to będzie banał a ja już nie pamiętam jak to sie robiło bo poziom pytania liceum.
Mamy zbiór 104 kart. Losujemy na raz 3 karty z tych 104. Kart dających wygrana z tego zbioru jest 19. Jakie jest prawdpodobienstwo że z, wylosowanych 3 kart przynajmniej jedna będzie wygrana? A jakie ze dwie będą wygrane?
- 0
- 3
- 1
- 0
Taką miałem rozkminę ostatnio pod prysznicem, może ktoś mi wytłumaczy:
1. Czy dyfuzja wynika jedynie z tego, że stan gdzie cząsteczki są w miarę równomiernie rozłożone można realizować na najwięcej sposobów (a zatem najwyższe prawdopodobieństwo takiego stanu)? Czy jest jeszcze jakaś siła, która powoduje, że rozmieszczają się równomiernie?
2. A co w przypadku mieszania roztworów 2 różnych obojętnych cząsteczek: wyrównywanie
- 4
Czy jest jeszcze jakaś siła, która powoduje, że rozmieszczają się równomiernie?
@Noniusz: Statystyka. Wsyp kulki kolorowe kuli do pojemnika i nim potrząsaj.
A co w przypadku mieszania
- 1
#prawdopodobienstwo #matematyka
- 0
- 0
#python #programowanie #matematyka #prawdopodobienstwo
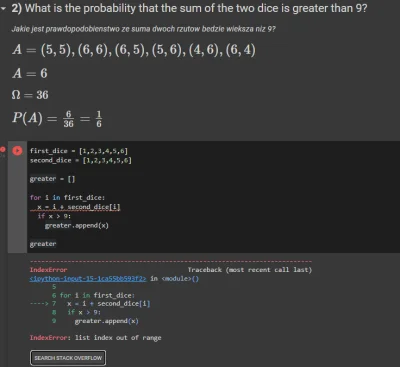
źródło: comment_1648487355mSF0LptcLYcs8eXhv88IBM.jpg
Pobierzw sensie - dostajesz element z kolekcji, a potem próbujesz nim jak indeksu szukać.
Jakbyś w firstdice miał na przykład [9,9]
To potem spróbujesz się odwołać do seconddice[9] => ?
- 0




























Komentarz usunięty przez autora