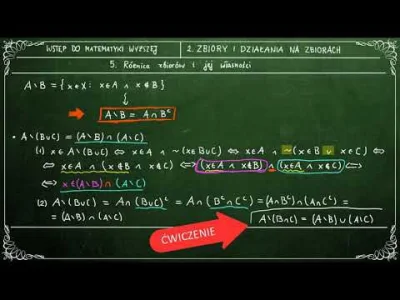
Właśnie odkryłem że twierdzenie de Lopitala to jest lim f/g = lim f'/g' zamiast lim (f/g) '
Od pierwszego kolokwium czułem że z drugim wzorem jest coś nie tak, bo zamiast pomagać tylko pogarsza... Szkoda strzelić ryja xd
#matematyka #studbaza
Od pierwszego kolokwium czułem że z drugim wzorem jest coś nie tak, bo zamiast pomagać tylko pogarsza... Szkoda strzelić ryja xd
#matematyka #studbaza
- Eldon4001
- adamopol
- konto usunięte
- Ominika
- konto usunięte
- +5 innych
@Scorpjon: najlepiej uczyć się całego materiału dzień/dwa dni przed kolosem, sprawdzone przy ostatnim kolokwium z całek więc na egzaminie też się uda xd
@siema_mordo: to moze de hospital? Xd bo taka była pierwsza wersja która kojarzę
@siema_mordo: to moze de hospital? Xd bo taka była pierwsza wersja która kojarzę
@razenas: de l’Hospitala, ale no fonetycznie można zapisać de lopital, wiec sie nie #!$%@? sorki memorki trzymaj się i powodzenia












































Krótka przypowieść o polskim szkolnictwie wyższym:
Po skończeniu liceum ogólnokształcącego, takiego zwykłego, postanowiłem iść w komputry, bo z tego są pieniądze, a w ogóle to lubiłem komputry, składałem komputry i ogółem znałem się, instalowałem sąsiadom lewe windowsy, ciągnąłem kable po osiedlu, konwertowałem filmy z DVD na Divx, no młody geniusz, dzisiaj osiedlowi Janusze nazwaliby mnie Jobsem.
Nie miałem matury z matmy, bo z matmy to noga byłem. W gimnazjum patola, braki
¯\(ツ)/¯
STUDIA TO NIE JEST OBOWIĄZEK
oraz
STUDIA NIE SĄ DLA KAŻDEGO
A o tym, jakim kto jest człowiekiem, nie świadczy jego wykształcenie, zarobki itd. itp.
EOT