Wszystko
Najnowsze
Archiwum
- 4
#budownictwo #nauka #matematyka

źródło: Zdjęcie z biblioteki
PobierzKomentarz usunięty przez moderatora
- 7

źródło: 1000006178
Pobierz6
Klasyfikator bayesowski, naiwność, m-estymata...

klasyfikacja tekstów, atrybuty nominalne i numeryczne. Wstęp do AI.
z- 1
- #
- #
- #
- #
- #
- 2

źródło: temp_file156271398942583002
Pobierz- 76
4
Skąd wziął się, znany nam dzisiaj, zapis cyfr?

Jakie inne zapisy istniały wcześniej? Na te pytania znajdziesz odpowiedź w filmie [Eng].
z- 0
- #
- #
- #
- #
- 4
- 3
5
Ciąg Eulera na spirali liczb

Ciąg Eulera jest wyjątkowy, ponieważ początkowe 40 wyrazów tego ciągu to liczby pierwsze. Tak wyglądają początkowe...
z- 0
- #
- #
- #
- 10
#matematyka #heheszki

źródło: matma
PobierzTa sie poplakala i poszla do dyrki. Matka wezwana na dywanik. Siedzimy w gabinecie i dyrka mowi ze tak nie mozna itp. A matka grzecznie pyta czy tam byl blad i czy ja jakos
10
Spirala liczb

Nie wiem, czemu Stanisław Ulam opublikował lewoskrętną spiralę zaczynającą się od 1 zamiast spirali prawoskrętnej...
z- 23
- #
- #
- 1
niestety chyba wszystkie format wprowadzania danych TYLKO format txt :-(

źródło: 577782695_122147587130841036_2063770427263751619_n
Pobierzdo algebry liniowej
@zrzed: a co chcesz konkretnie zrobić i po co Ci llmy do tego skoro od dziesiątek lat istnieją lapacki/linpacki/blasy/wolframy itp, które Ci wszystko policzą i nawet krok po kroku pokażą
- 0
inaczej nie wrzucisz do ai
np

źródło: ascii-art-powerpoint-template-slide
PobierzA medycyna? To jest żart. Naucz się 206 kości w ciele czlowieka. Wykuj na pamięć kilkudziesiat chorob pasożytniczych.

źródło: Zdjęcie z biblioteki
Pobierz- 5
- 16

źródło: 1000006143
Pobierz- 16
Podstawowy powód jest taki, że na palcach da się policzyć tylko do 19, a w dwunastkowym, na paliczkach da się policzyć nawet do 500 (720 w systemie dziesiętnym). Zobaczcie przygotowaną ilustrację, jak to wyglądało.
Dla łatwości przyjjęłam system dwunastkowy jako 1,2,3,4,5,6,7,8,9,a,b,10 aby ładnie było widać dziesiątki (tak naprawdę to się nazywało tuziny) i setki (tuziny tuzinów - czyli gros).
To

źródło: temp_file1151966171692943266
Pobierz
źródło: matura
Pobierz- 11

źródło: 1000006139
Pobierz- 1
Kto z poniżej podanych osób ma fajniejszą przestrzeń?
- Doniu 35.3% (6)
- Banach 64.7% (11)
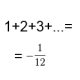























źródło: ech
Pobierz