#astronomia #ciekawostki #dragonspamuje #eioba #kosmos
Wszystko
Wszystkie
Archiwum
4
Portal Eioba.pl został wykupiony
za artykuł dnia stawka 100 zł, artykuł tygodnia - 300 zł, a za artykuł miesiąca - 800 zł
z- 4
- #
- #
- #
- #
- #
- #
#astronomia #ciekawostki #dragonspamuje #eioba #kosmos
źródło: comment_VtzvoDKT6GJAajczcC081YNCdcVWNPPC.jpg
Pobierz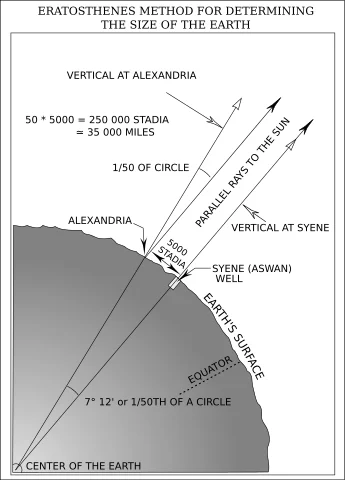
źródło: comment_ZpJfx4omf1YhYQFotgFxSU7NHPMmstaT.jpg
Pobierz- 0
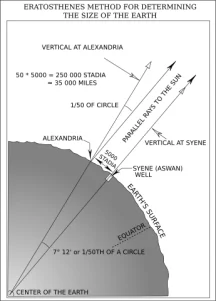
Eratosthenes calculated the circumference of the Earth without leaving Egypt. Eratosthenes knew that at local noon on the summer solstice in the Ancient Egyptian city of Swenet (known in ancient Greek as Syene, and now as Aswan) on the Tropic of Cancer, the Sun would appear at the zenith, directly overhead. He knew this because he had been told that the shadow of someone looking down a deep well in Syene would block the reflection of the Sun at noon off the water at the bottom of the well. Using a gnomon, he measured the Sun's angle of elevation at noon on the solstice in Alexandria, and found it to be 1/50th of a circle (7°12') south of the zenith. He may have used a compass to measure the angle of the shadow cast by the Sun.[16] Assuming that the Earth was spherical (360°), and that Alexandria was due north of Syene, he concluded that the meridian arc distance from Alexandria to Syene must therefore be 1/50th of a circle's circumference, or 7°12'/360°.
His knowledge of the size of Egypt was founded on the work of many generations of surveying trips. Pharaonic bookkeepers gave a distance between Swenet and Alexandria of 5,000 stadia. Some say this distance was corroborated by inquiring about the time that it took to travel from Syene to Alexandria by camel. Carl Sagan says that Eratosthenes paid a man to walk and measure the distance. He rounded the result to a final value of 700 stadia per degree, which implies a circumference of 252,000 stadia. Some claim Eratosthenes used the Egyptian stade of 157.5 meters, which would imply a circumference of 39,690 km, an error of 1.6%, but the 185 meter Attic stade is the most commonly accepted value for the length of the stade used by Eratosthenes in his measurements of the Earth,[17] which imply a circumference of 46,620 km, an error of 16.3%. It is unlikely, however, that Eratosthenes got an accurate measurement of the circumference of the Earth, given three errors in the assumptions he
859
Tak powstają niektóre artykuły, które czytasz w necie
Problem dotyczy nie tylko dziennikarstwa społecznościowego. Również pracownicy (bo nie nazwę ich redaktorami) poważnych serwisów z newsami działają w taki sam, albo podobny sposób...
z- 116
- #
- #
- #
- #
- #
- #
- #
- #
33
Kilka porad dla bezrobotnych absolwentów
Twojego pracodawcę zupełnie nie interesuje ile masz kwitów poświadczających wyższe wykształcenie, tylko to ile będziesz potrafił zarobić pieniędzy dla firmy, która Cię zatrudni.
z- 32
- #
- #
- #
- #
- #
- #
- #
- #
11
O inteligentnych inaczej
Przepraszam, czy to koniec kolejki? - Nie, to początek, tylko wszyscy tyłem stoimy.
z- 1
- #
- #
- #
8
Naj...cz 2
- 1
- #
- #
- #
- #
6
Czy my ze sobą naprawdę rozmawiamy?

O tej szczerej, prawdziwej rozmowie słów kilka.
z- 0
- #
- #
- #
- #
- #
- #
- #
- #
- #
8
G---o TV
- 0
- #
- #
- #
5
Jak Eioba traktuje autorów?
Eioba mieni się serwisem poważnym, z wartościową treścią. W praktyce masa tam kopii z innych stron, masa treści bez interpunkcji i z błędami. No i zapomnij o linku bez nofollow, to wg Eioba za duża zapłata za trud...
z- 0
- #
- #
- #
21
Foch jako efektywna metoda zarządzania mężczyzną
Mała charakterystyka tego zjawiska:) Dla mężczyzny dokształcenie z szczyptą humoru, a dla kobiet odrobina dystansu wobec samych siebie:)
z- 13
- #
- #
- #
- #
- #
- #
6
Kraj Kwitnących Absurdów
Patrząc na Polske bez emocji i uprzedzeń dochodzę do wniosku, że nasz kraj jest pietrzącą sie piramidą absurdu i trudnej do wytłumaczenia głupoty
z- 0
- #
- #
- #
- #
- #
5
Urodzić się jako oryginał
- 1
- #
- #
- #
- #
122
Mleko - białe kłamstwa
Nawet 100 milionów ciałek ropnych w każdej szklance... to wystarczający powód, by odstawić mleko. Dla zdrowia.
z- 111
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4
Alchemia miłości
Dlaczego kobieta, wchodząc do pustego kina, wybiera krzesło, na którym niedawno siedział mężczyzna? Dlaczego mężczyzna, patrząc na rząd, równie atrakcyjnych, podobnych do siebie kobiet, czuje pociąg do jednej, a obojętność do innej? Odpowiedź tkwi w feromonach. Sztuka w trzech aktach.
z- 0
- #
- #
- #
- #
- #
- #
- #
- 1
8
Jak pokonać bezsenność?
- 2
- #
- #
- #
- #
- #
- #
- #
- #
8
Ironia Ironii - abominalne piękno.
"Wszystko jest niewyraźne do poziomu którego nie jesteś nawet świadom, dopóki cośtam cośtam cośtam..."
z- 0
- #
- #
- #
- #
- #
6
Tekst Krzysztofa Kubasiewicza na Eiobie i wymiana zdań z autorem.
"Księżycowa gospodarka w rolnictwie?..." czyli dlaczego Krzysztof Kubasiewicz ( Startował do sejmu z ramienia Samoobrony , redaktor naczelny radia Parada w Łodzi, właściciel browaru Bojanowo, dużego gospodarstwa prowadzącego chów świń w Byszewie w gm. Kutno, stadniny ogierów w Prądzewie koło Łęczycy ) nie lubi małych gospodarstw rodzinnych.
z- 1
- #
- #
- #
- #
5
Sami zarobią, a zarobić nie dadzą
Serwisy społecznościowe w Naszym kraju mają się dobrze. Dzięki Nam zarabiają duże pieniądze, ale same zarabiać nie dadzą swoim użytkownikom. Wszystkiemu winny jest Nasz naród, w którym panuje przekonanie, że skoro mi jest źle, to innym też musi być źle. Marudzenie, narzekanie i kopanie dołków pod sąsiadem stało się Naszą narodową tradycją.
z- 0
- #
- #
- #
- #
- #
- #
- #
- #



#gownowpis #wykop #eioba