Tak apropo dyskusji w temacie #matura która szaleje na wykopie to może się wypowiem jako tegoroczny maturzysta.
1) Matura nie jest wszystkim potrzebna. Społeczeństwo i pracodawcy stworzyli taki rynek i ludzie się do niego dostosowują. Wszędzie, jako młody człowiek, jesteś atakowany informacjami, że potrzebujesz wykształcenia, a jak chodzisz do lepszej szkoły gdzie chodzisz z dziećmi bogatych rodziców to ci rodzice powiedzą ci, że nie jest potrzebna. I w






















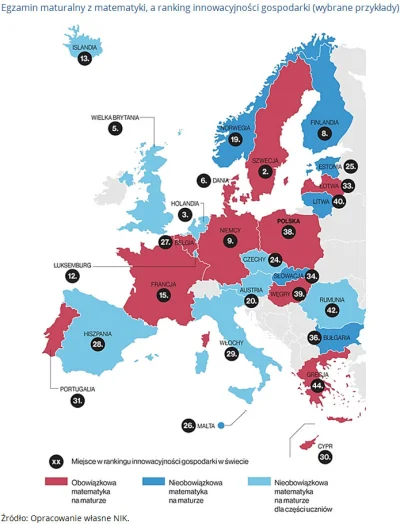














#matematyka #matura
źródło: comment_eAS9vU9pk2glOggCR0TkMf2GyeNJER03.jpg
Pobierz@wonsz_smieszek: To mi pomogło, dzięki wielkie.