Pytanie takie do matematycznych świrów. Wzór na odwzorowanie liniowe należy podawać w bazach kanonicznych czy w dowolnych bazach? Tzn. jest w zadaniu macierz odwzorowania oraz bazy względem których zapisano tę macierz. Polecenie jest aby podać wzór na odwzorowanie. Teraz powinienem po prostu przemnożyć macierz przez wektor i mieć wzór, czy przekształcić macierz na bazy kanoniczne?

#matematyka #algebra #agh

Potrzebuję pomocy z logiki, a tak się składa że wszystko co związane z matematyka itd. jest dla mnie czarną magią. Chodzi mi o schematy zdań mianowicie mam zdania, które brzmią:

Kto szybko daje, ten dwa razy daje oraz kto nie ma miedzi, ten w domu siedzi. Obydwa są ogolno twierdzące jednak mam problem ze wskazaniem podmiotu i orzecznika, wydaje mi się że w pierwszym podmiotem jest osobą szybko dająca a orzecznikiem osobaPokaż całość

Halko, ogarnia ktoś tu algebrę abstrakcyjną (te podstawowe rzeczy - grupy, monoidy sridy itp.) albo ma jakieś źródło gdzie ładnie jest to wytłumaczone? #studbaza #algebra #matematyka

#etrapez #matematyka Czy znajdę gdzieś na internecie etapy rozwiązywania zadań do prac domowych z etrapeza, nie chodzi mi o same odpowiedzi?

Wymyśliłem tak z nienacka, śmieszne i zabawne trochę w sumie kodowanie lub szyfrowanie. Kwestia podejścia chyba.

Ciekawe na ile ktoś wpadnie jak to działa i zdekoduje ciągi znaków na końcu lub obmyśli metodę jak to działa

Tutaj przykładowo zakodowane wyrazy (tylko wyrazy ponieważ dla samych wyrazów to zaimpementowałem):

(JakPokaż całość

Na jaki ścisły kierunek można iść tak just for fun?

Znajoma na weterynarii. Poszła z zamiłowania, mimo tego że zawsze najlepiej czuła się w przedmiotach ścisłych. Powoli już kończy wetę, ale męczy ją zakuwanie działania leków i trochę tęskno jej za matmą. Szuka czegoś czym by mogła się zająć jako odskocznia. Raczej bez celów zarobkowych bo planuje zostać wetem.

Inb4 informatyka odpada.Pokaż całość

Cześć.

Mam takie głupie pytanie, ale... jak się rozwiązuje z matematyki cięższe, nieschematyczne zadania? Wiem, że głupio to brzmi o mnie, ale naprawdę nie wiem jak się do takich zabrać ;/ Umiem robić tylko takie zadania, których schemat był pokazany na lekcji.

Przykładowo, takie zadanie z Olimpiady Matematycznej dla gimnazjów.
Liczby p i q są różnymi liczbami pierwszymi. Udowodnij, że liczba p 2 + q 2 nie jest podzielna przez liczbę p + q.Pokaż całość

co ta główna

#matematyka

#matematyka
Czy jeśli funkcja f jest w L^2 (0, 1) to całka z f jest w L^1(0,1)?

Nie ważne, czy w systemie dziesiętnym, czy binarnym, pierwiastek kwadratowy ze 100 i tak jest 10.
#ciekawostki #matematyka

#humorobrazkowy #pokemon #matematyka #heheszki

Mirki, mirabelki i idioci.
Mam problem wagi ciężkiej.
Jak k---a 0,75 jest dobrą odpowiedzią jak nie jest

#egzaminzawodowy #technikum #szkola #matematyka

Kojarzy ktoś ten znak? Poda jego nazwę lub napeowidzi jak go wstawić w tekst?
( ͡° ͜ʖ ͡°)

#matematyka #informatyka #office #komputery #pytanie #zapytaj

podjąłem decyzję: nauka fizyki od zera już teraz, matematykę rozszerzoną od razu po podstawie, czyli maks za tydzień.

UPRZEDZAM: jestem na mat-geo, chcę iść na informatykę do Lublina i na samej matmie byłoby mi się ciężko dostać, dlatego chciałbym napisać fizykę nawet na te kilkanaście procent, dużo większe szanse. Do tego jeszcze rozszerzony angielski na trochę, może dam radę XD

#matura #fizyka #matematyka

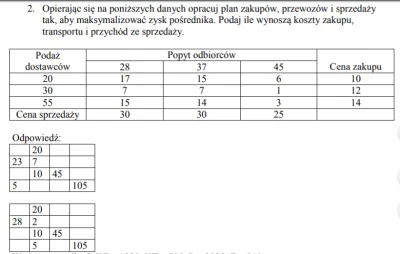
Mirki, czy ktoś jest mi w stanie pomóc i wytłumaczyć jak krowie na rowie zadanie pośrednika? Czym to się różni od zwykłego zadania transportowego? Polecenie poniżej, nie wiem nawet od czego tu zaczynać, normalnie jak zadanie transportowe tylko potem po prostu manipulować wszystkim tak, żeby koszt zakupu i transportu był jak najmniejszy, a dochód ze sprzedaży jak największy?

Dodatkowo mam pytanie o zadanie transportowe. Polecenie brzmi: "Rozwiąż poniższe zadanie transportowe metodą potencjałówPokaż całość

Dla wszystkich co to się pytają "a czy matma się mi przyda w życiu".
#heheszki #matematyka

Nie każdy bohater nosi pelerynę. Dziękuje panie Matemaks 乁(♥ ʖ̯♥)ㄏ

#heheszki #matematyka #matura

Pamietam ze przy funkcjach w gimbazie zaczely sie problemy, a dalej to juz naprawde nie mialem pojecia o czym do cholery na tych lekcjach p------a. K---a jakies wzory, iksy dupiksy, objetosci k---a s--------c z tym gownem co mnie to k---a obchodzi
#matematyka #matura #nauka

Pokaż spoiler