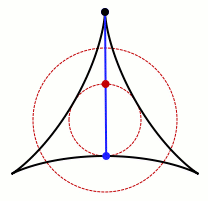
Wyobraźmy sobie igłę umieszczoną wewnątrz pewnego zbioru na płaszczyźnie. Igłę traktujemy jak odcinek jednostkowy, który możemy dowolnie obracać i przesuwać w obrębie naszego zbioru. Załóżmy, że chcielibyśmy wykonać igłą obrót o 360 stopni – jak wiele miejsca do tego potrzeba? Pytanie to zadał po raz pierwszy japoński matematyk Soichi Kakeya w 1917 roku a zaskakującej odpowiedzi udzielił Abraham Besicovitch w 1919 roku. Okazuje się, że można skonstruować zbiór o zadanej własności mający
- Muszalski
- konto usunięte
- wow
- gzem89
- konto usunięte
- +61 innych
@asztar: Połóż igłę na stole i spróbuj ją obrócić dookoła tak, żeby jej końce zakreśliły jak najmniejszy obszar.
Na przykład pierwszym sposobem, jaki się nam nasuwa, jest zwykłe zakręcenie - końce igły zakreślą okrąg. Można trochę to ulepszyć i wykorzystać trójkąt równoboczny o boklu długości igły - to też nie jest trudne do wyobrażenia. Gif przedstawia nieco bardziej "zaawansowany" sposób - mamy pole mniejsze niż pole trójkąta równobocznego.
Natomiast Besicovitch wykazał,
Na przykład pierwszym sposobem, jaki się nam nasuwa, jest zwykłe zakręcenie - końce igły zakreślą okrąg. Można trochę to ulepszyć i wykorzystać trójkąt równoboczny o boklu długości igły - to też nie jest trudne do wyobrażenia. Gif przedstawia nieco bardziej "zaawansowany" sposób - mamy pole mniejsze niż pole trójkąta równobocznego.
Natomiast Besicovitch wykazał,
- asztar
- konto usunięte
- konto usunięte
- prusi
- robko
- +4 innych
Można trochę to ulepszyć i wykorzystać trójkąt równoboczny o boklu długości igły
@scyth: *o wysokości długości igły
- scyth
- konto usunięte
- konto usunięte
- Rzuku
- Talar_
- +1 innych



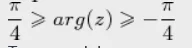










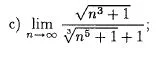



















#matematyka #studbaza #studbazaproblems #jestemidiota
http://i.imgur.com/NlZpcxz.gif
x. A tak naprawdę jest tam
|x|, co ma duże znaczenie biorąc pod uwagę, że
x-> - ∞