
- konto usunięte
- konto usunięte
- konto usunięte
- konto usunięte
- Brisign
- +2 innych
Wszystko
Wszystkie
Archiwum


11

Proste do zdefiniowania i zrozumienia problemy geometr. często są trudne do rozwiązania i wymagają użycia skomplikowanych algorytmów. Weźmy, na przykład, zadanie polegające na znalezieniu największego okręgu, który możemy zmieścić w wielokącie. Środek tego okręgu nazywany jest środkiem Czebyszewa.
z

7

Przykład zaczerpnięty z książki "Śladami Pitagorasa" Warty uwagi z racji tego, że stawia pomost pomiędzy algebrą i geometrią.
z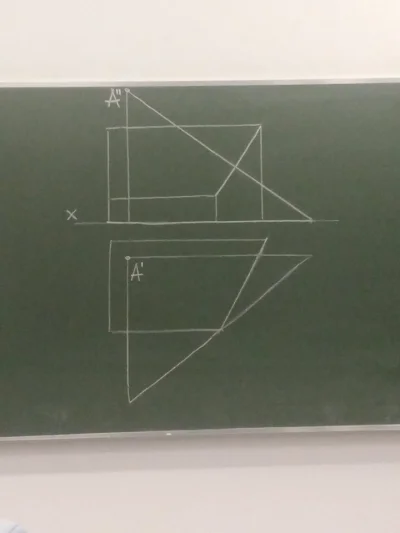
14
Przykład z książki "Śladami Pitagorasa" Ciekawe połączenie geometrii z algebrą na przykładzie mnożenia.
z20
![Paradoks Banacha-Tarskiego [ENG, z napisami]](https://wykop.pl/cdn/c3397993/link_iSzcT7bwNW1GGsoqhj0YWnO8wSgU6LEA,w220h142.jpg)
Autor filmu w prosty i obrazowy sposób udowadnia twierdzenie Banacha-Tarskiego o paradoksalnym rozkładzie kuli. Nie używa się żadnego formalizmu matematycznego, a wszystkie potrzebne pojęcia są wyjaśnione w pierwszej części filmu. Po angielsku, ale z napisami
z

Komentarz usunięty przez autora
7
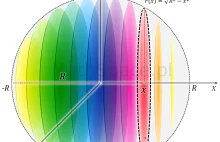
"Jak oczami wyobraźni zobaczyć 4 wymiary? - zapytano matematyka. To proste - odpowiedział - wystarczy wyobrazić sobie n-wymiarów i podstawić n=4" - Jak w zależności od liczby wymiarów zmienia się powierzchnia i objętość kuli? - Jak zmienia się maksymalna odległość pomiędzy wierzchołkami kostki?
z
Wykop.pl