konto usunięte via Android
#heheszki #matematyka #geometria #gwo
- fajnylogin
- TheQuake
- Andrzej_galazka
- Cronox
- 77LatBedeNiedojrzaly
- +1 innych
Wszystko
Wszystkie
Archiwum
więcej niz zbieg okoliczności z 1609 roku [ENG]
![więcej niz zbieg okoliczności z 1609 roku [ENG]](https://wykop.pl/cdn/c3397993/link_qgWomcGJ6hrnzZbADnumBjCkWie6vp43,w220h142.jpg)
Zaskakująca geometria w sonetach Szekspira. Co z niej wynika? Obejrzyjcie sami.
z- 4
- #
- #
- #
jakie to piękne, najpierw do mechaniki kwantowej trzeba było wyjść poza "klasyczną" #matematyka i #geometria (liczby urojone, zespolone, geometria nieprzemienna, dodatkowe wymiary, hamiltoniany, tensory, ...) a teraz #fizykakwantowa wraca z powrotem do matematyki aby spróbować rozwiązać jeden z problemów milenijnych dot. hipotezy Riemanna (https://www.wikiwand.com/pl/Hipoteza_Riemanna). Dodam od siebie, że owa hipoteza ma niezerową wartość ludzi, którzy oszaleli na jej punkcie, co przyczyniło się do ich śmierci - jest film na yt.
http://www.sciencealert.com/this-paper-could-be-the-key-to-solving-a-160-year-old-million-dollar-maths-problem
http://www.sciencealert.com/this-paper-could-be-the-key-to-solving-a-160-year-old-million-dollar-maths-problem
- superblee66
- tyrald
- konto usunięte
- Ilmarinen
- konto usunięte
- +7 innych
Mam takie zadanko, nie za bardzo wiem jak się za nie zabrać ( ͡° ʖ̯ ͡°)
W prostokącie ABCD poprowadzono przekątną AC. Bok AD ma długość x, a bok AB x pierwiastka z 2. Przeprowadzono odcinek DS tak, że punkt S jest środkiem odcinka AB. Oblicz kąt między odcinkami DS i AC.
#zadanie #matematyka #geometria
W prostokącie ABCD poprowadzono przekątną AC. Bok AD ma długość x, a bok AB x pierwiastka z 2. Przeprowadzono odcinek DS tak, że punkt S jest środkiem odcinka AB. Oblicz kąt między odcinkami DS i AC.
#zadanie #matematyka #geometria
Andreth
@Tom_Ja: Trójkąt ACD - możesz policzyć kąt DAC? Możesz. Trójkąt ADS - możesz policzyć kąt ADS? Możesz. No a szukany kąt jest trzecim w trójkącie AOD (gdzie O jest punktem przecięcia DS i AC).
#autocad #studbaza troche #matematyka ale bardziej #geometria #techbaza #zagadki
Mirki mam trzy okręgi, a właściwie to trajektorie ruchu punktu po okręgu. Chodzi o to, żeby geometryczny środek odcinka leżał na środkowym okręgu, a dwa pozostałe równe końce o znanych wymiarach leżały na odpowiadających sobie okręgach. Ktoś ma pomysł jak i czy się tak w ogóle da zrobić?? Doraźnie poradzilem sobie dokładając kartkę papieru z zaznaczonymi odległościami i smyrając po ekranie, ale może
Mirki mam trzy okręgi, a właściwie to trajektorie ruchu punktu po okręgu. Chodzi o to, żeby geometryczny środek odcinka leżał na środkowym okręgu, a dwa pozostałe równe końce o znanych wymiarach leżały na odpowiadających sobie okręgach. Ktoś ma pomysł jak i czy się tak w ogóle da zrobić?? Doraźnie poradzilem sobie dokładając kartkę papieru z zaznaczonymi odległościami i smyrając po ekranie, ale może
@spinel: Sposób wykonania dowolny, nie ma nic oprócz danych kółek i wymiaru pręta
Mirki, pomóżcie z geometrią. Dlaczego żeby obliczyć gamme muszę wziąć akurat miarę tego kąta? Zadanie proste, ale zastanawia mnie to od dłuższego czasu.
#matematyka #geometria #licbaza
#matematyka #geometria #licbaza
@MaIutkiCzlowiek: @Sayec: O kurde panowie, dzięki za pomoc. Rozwiązanie miałem kilka stron dalej w podręczniku. Dziękuję za fatygę.
Mirki czy taka figura ma swoją nazwę? Wiem, że nie narysowane dokładnie, ale chodzi mi o połączenie prostopadłościanu i ostrosłupa. #matematyka #nauka #geometria
@Strusiekmcze: dom
- dzangyl
- konto usunięte
- sprynek
- nilhir
- xyz23
- +10 innych
konto usunięte via Android
@KacasPiesel tak jak narysowałeś masz trójkąt odbity, ale nie przystający. Chodzi o to, że żeby dopasować trójkąt do przystającego mu trójkąta możesz jedynie obracać go (zgodnie z ruchem/przeciwnie że wskazówkami) a nie odbijać względem boku.
#matematyka #geometria
Ma ktoś pomysł, jak pokazać, że środek okręgu dziewięciu punktów jest w połowie odległości HO (H - ortocentrum, O - środek okręgu opisanego na tym trójkącie)?
Ma ktoś pomysł, jak pokazać, że środek okręgu dziewięciu punktów jest w połowie odległości HO (H - ortocentrum, O - środek okręgu opisanego na tym trójkącie)?
@kolnay1: Jakby co to znalazłem już w Prasolovie
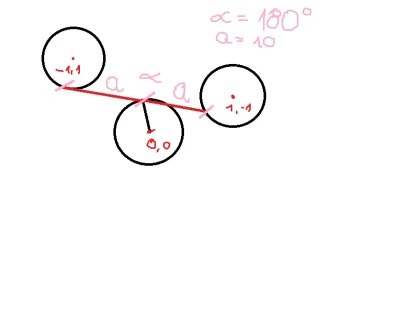
The homothety with center H and coefficient 1/2 sends the circumscribed circle of triangle ABC into the circumscribed circle of triangle A3B3C3 (u mnie to SaSbSc) , i.e., into the circle of 9 points. Therefore, this homothety sends point O into the center of the circle of nine points
Uogólnione twierdzenie Pitagorasa - mało znana wersja, nieco zaskakująca :-)
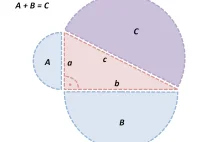
Okazuje się, że twierdzenie Pitagorasa można rozszerzyć na klasę wielu kształtów, o ile spełnione są odpowiednie warunki podobieństwa figura. Obrazek wszystko wyjaśnia.
z- 1
- #
- #
Wyznacznik macierzy - przedstawiona super interpretacja geometryczna + animacje
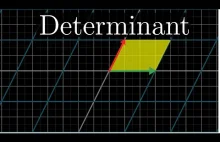
Analizowane jest przekształcenie liniowe opisane macierzą przekształcenia liniowego. Wyznacznik takiej macierzy reprezentuje "współczynnik skalowania" pola powierzchni / objętości / miary obiektu transformowanego przekształceniem liniowym. Świetne animacje :-) Polecam!
z- 3
- #
- #
- #
@JackMaster: sketchup. nic prostszego chyba nie znajdziesz, a zrobisz w nim wszytko co sobie wymyślisz (masa dodatków) albo ściągniesz z gotowej biblioteki modeli.
@JackMaster: najłatwiejszy jaki w życiu spotkałem jest Autodesk 123D = http://www.123dapp.com/design
Ale jak masz marnować czas na przystosowanie się do 123D a później kląć że czegoś brakuje to zacznij od razu od sketchupa.
Ale jak masz marnować czas na przystosowanie się do 123D a później kląć że czegoś brakuje to zacznij od razu od sketchupa.
#politechnika #budownictwo #geometria #geometriawykreslna #politechnikapoznanska
Czy jest tu ktoś ogarniający geometrię wykreślną i chciałby zarobić? ( ͡€ ͜ʖ ͡€)
Czy jest tu ktoś ogarniający geometrię wykreślną i chciałby zarobić? ( ͡€ ͜ʖ ͡€)
@ptasiek2: przenikanie wieloscianów mozna zrobić w autocadzie a rozwinięcią nawet nie komentuje ( ͡° ͜ʖ ͡°)
Matka natura i jej matematyczna figura geometryczna
- 15
- #
- #
- #
- #
- #
- #
Niezwykły zagadkowo logiczny sześcian
Autor prezentuje jedną z najlepszych zagadek logicznych w swojej kolekcji w postaci sześcianu.
z- 3
- #
- #
- #
- #
- #
- #
Mirki z tagu #programowanie
bo się trochę zapętliłem już i nie ogarniam :(
To pewnie banalnie proste ale już się zakręciłem totalnie.
mam punkt w przestrzeni w której znajduje się dowolna bryła
z punktu "strzelam" półprostą w dowolnym kierunku.
I stąd moje pytanie:
Jak najłatwiej sprawdzić, czy prosta przebija jakąś z płaszczyzn, które składają się na bryłę?
#matematyka #geometria
bo się trochę zapętliłem już i nie ogarniam :(
To pewnie banalnie proste ale już się zakręciłem totalnie.
mam punkt w przestrzeni w której znajduje się dowolna bryła
z punktu "strzelam" półprostą w dowolnym kierunku.
I stąd moje pytanie:
Jak najłatwiej sprawdzić, czy prosta przebija jakąś z płaszczyzn, które składają się na bryłę?
#matematyka #geometria
@SzCzoteckY: No panie, jeśli strzelasz półprostą, tzn masz jej równanie.
Jeśli masz bryłę, tzn masz równanie którym jest opisana. Rozzwiązujesz powstały układ równań i patrzysz ile ma rozwiżań.
Jeśli masz bryłę, tzn masz równanie którym jest opisana. Rozzwiązujesz powstały układ równań i patrzysz ile ma rozwiżań.
@Jare_K: rzut środkowy tu nie bedzie pasował bo musze określić, czy punkt w którym zaczyna się pół prosta jest w bryle czy poza nią.
Geometria w najlepszym wydaniu ! (｡◕‿‿◕｡). Potęga nauki jest nieograniczona ◕‿◕
#ciekawostki #nauka #dziwniesatysfakcjonujace #geometria
#ciekawostki #nauka #dziwniesatysfakcjonujace #geometria
- konto usunięte
- konto usunięte
- cykus
- alkan
- lord_100
- +7 innych
#matematyka #geometria
http://i.imgur.com/lKg3eVu.png
Może ktoś z was to wymyśli, bo pytanie wydaje się łatwe, a już nie mam pomysłu i nie mogę na to patrzeć. Chciałbym pokazać, że kąty OCOb i OAOb są proste, bo tylko tej pierdoły mi brakuje do tego żeby pokazać, że odcinki OM i MOb są sobie równe. Równość AM, OM i MC już pokazałem, a docelowo trzeba pokazać, że A,O,C,Ob leżą na jednym okręgu o środku w
http://i.imgur.com/lKg3eVu.png
Może ktoś z was to wymyśli, bo pytanie wydaje się łatwe, a już nie mam pomysłu i nie mogę na to patrzeć. Chciałbym pokazać, że kąty OCOb i OAOb są proste, bo tylko tej pierdoły mi brakuje do tego żeby pokazać, że odcinki OM i MOb są sobie równe. Równość AM, OM i MC już pokazałem, a docelowo trzeba pokazać, że A,O,C,Ob leżą na jednym okręgu o środku w
@BazaltowyTubylec: Styczny do jednego z boków trójkąta (w tym wypadku AC) i do przedłużeń pozostałych. Może dodam, że środek takiego okręgu też jest wyznaczony przez dwusieczne odpowiednich kątów, tylko w przypadku tych gdzie były brane przedłużenia boków trzeba brać pod uwagę ich dopełnienia. W skrócie jest to to co widać na rysunku ;)
Jakby co to wyszło mi w końcu to zadanie, ale chyba mocno naokoło.
Dobry wieczór, jak takie zadanie zrobić bo nie wiem, a bardzo bym chciał wiedzieć.
halp.
#matematyka #geometria
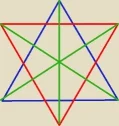
Trójkąt A'B'C' jest obrazem trójkąta równobocznego ABC w jednokładności o środku w punkcie
przecięcia dwusiecznych trójkąta ABC i skali k= −1. Oblicz pole części wspólnej tych figur,
wiedząc, że bok trójkąta ABC ma długość 12.
halp.
#matematyka #geometria
@dzony_: Poprawiam. Jeśli to jest co najmniej jedna para boków równoległych to może to być:
- prostokąt (jeśli druga para również jest równoległa)
- kwadrat (jeśli druga para również jest równoległa oraz tej samej długości co pierwsza para)
- trapez równaramienny (wsztstkie inne sytuacje).
We wszystkich figruach przekątne są tej samej długości.
- prostokąt (jeśli druga para również jest równoległa)
- kwadrat (jeśli druga para również jest równoległa oraz tej samej długości co pierwsza para)
- trapez równaramienny (wsztstkie inne sytuacje).
We wszystkich figruach przekątne są tej samej długości.