Wszystko
Najnowsze
Archiwum
Z tego co wiem to w tym modelu nie da się ich regulować. Żeby to poprawić musiałbyś wymienić wahacze, mocowania amortyzatora, amortyzatory a na koniec i tak by się okazało ze z upływu lat to się buda wypaczyła a nie zawiecha.
Jeździć, obserwować.
W takich małych autach o prostym zawieszeniu na kąty PK i WSW bardzo wpływa obciążenie. Wystarczy że fotel kierowcy nie był obciążony 75 kg i już wychodzą poza normą. O ile zbieżność jest ok to nie ma co się przejmować.
W geometrii sferycznej trójkąt ma wszystkie kąty proste.
@oleeeck:
W geometrii sferycznej ISTNIEJE trójkąt, który ma wszystkie kąty proste.
Generalnie istnieją trójkąty o kątach od 180 do 360.
#chwalesie bo obraz powędrował do jednego Mireczka a przy tym zasilił moją studencką kieszeń, pozdrawiam cieplutko ( ͡° ͜ʖ ͡°)
Płótno 30x40cm, farby akrylowe
#kosmos #tworczoscwlasna #malarstwo #rysujzwykopem #malujzwykopem #
źródło: comment_MPzlbckWxr1Z5WbslTIbgDVBagFC5NUJ.jpg
Pobierz
Matematyka zadanie z Parowozikiem, który wjeżdza na...
Ciekawa łamigłówka matematyczna dla każdego. #matematyka #geometria #zadanie
z- 1
- #
- #
- #
- #
- #
- #
Uszanowanko,
mam do policzenia coś takiego jak na obrazku poniżej. Dana jest mi jedynie odległość a oraz b, czy w takich warunkach jestem w stanie obliczyć pole czerwonego wycinka? Jeśli nie, to czego jeszcze potrzebuję lub jak bez używania przyrządów mierniczych to wyliczyć. Będę wdzięczny również za wskazówki ( ͡º
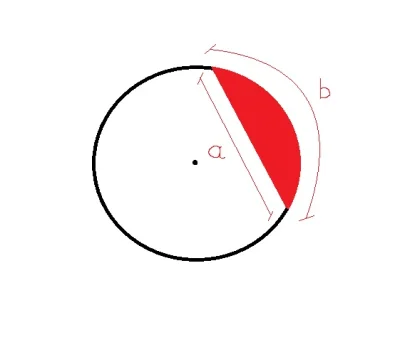
źródło: comment_ZNcx9LS5hZ0dow4DkjYAH4m8Hxte9Q2M.jpg
Pobierz
Komentarz usunięty przez autora
tu są wzory, jest wzór na długość łuku, jest wzór na długość cięciwy, robisz sobie układ równań, z których wyznaczasz sobie kąt środkowy oparty na łuku i promień koła i powinno pójść już
Mapa na spirali Eulera
Ponieważ Ziemia jest kulą, jej powierzchni nie da się odwzorować na płaszczyźnie bez zniekształceń. Matematyczka Hannah Fry opowiada o pewnym nietypowym sposobie, pozwalającym ułożyć powierzchnię kuli na płaszczyźnie, udowadniając go przy pomocy obieranej pomarańczy.
z- 2
- #
- #
- #
- #
- #
#natura #geometria #ciekawostki #zima
źródło: comment_6bqFQ6bMBh2ZntVN4Pu3Wg88t9VY3yXH.jpg
PobierzPetarda - jak gif! ( ͡° ͜ʖ ͡°)
Obrazków raczej nie wykopuje, ale ten muszę. Tak dobrej ngrafiki jeszcze nie widziałem!
z- 1
- #
- #
- #
- #
- #
Problem przesunięcia sofy
Jakie jest maksymalne pole sofy, którą można przesunąć przez korytarz w kształcie litery L o jednostkowej szerokości? - taki problem sformułował ponad 50 lat temu austriacko-kanadyjski matematyk Leo Moser...
z- 0
- #
- #
- #
- #
- #
- #
Badacze japońskiego uniwersytetu rozwiązali 2000-letni problem matematyczny.
Naukowcy z Uniwersytetu Keio rozwiązali problem istnienia pary unikalnych trójkątów prostokątnego i równoramiennego o tym samym obwodzie i obszarze. ENG
z- 5
- #
- #
- #
- #
- #
- #
Podręczniki do wymiany? Oto nowy geometryczny środek Polski.
Zdaniem naukowców to nie we wsi Piątek znajduje się geometryczny środek Polski. Ich zdaniem centralny punkt kraju jest oddalony o 17 kilometrów dalej i jest w miejscowości Nowa Wieś. Władze gminy Piątek nie uznają badań naukowców.
z- 87
- #
- #
- #
- #
- #
Geometria Bolyaia-Łobaczewskiego - co to jest i jak ją poznawać
Najdłużej badanym problemem mat. była kwadratura koła. Zaraz za nią uplasowała się kwestia piątego postulatu Euklidesa. Na początku XIX w. J. Bolyai i N. Łobaczewski, uparli się, by świat przyjął, że usunięcie piątego postulatu nie tyle narusza gmach geometrii, co go dość gruntownie przebudowuje...
z- 1
- #
- #
- #
- #
- #
A więc jednak, zadałem pytanie na allegro. Treść wiadomości
Dlaczego parametr "H" jest krótszy od "G". Czy w tabeli jest błąd? Przecież długość drabiny będzie zawsze dłuższa od wysokości względnej na której chcę pracować...
Taka odpowiedź:
"wysokość G - odnosi się do wysokości roboczej (czyli zasięgu jaki jest Pan w stanie osiągnąć stojąc na
Witam! Znacie jakiś porządny warsztat który zajmuje się ustawianiem geometrii/zbieżności? Szukam na terenie Śląska, najlepiej w okolicach #jaworzno #myslowice #cabanow #katowice