Czy wytłumaczy mi ktoś łopatologicznie skąd wziął się logarytm naturalny, dlaczego jest tak ważny, i dlaczego ma akurat w swojej postawie liczbę e? W chemii fizycznej, termodynamice i przemianach gazu doskonałego, których się własnie uczę pojawia się cały czas... Ale dlaczego? To tylko artefakt matematyczny, czy jakaś rzeczywista wartość związana z fizyką?
Wszystko
Najnowsze
Archiwum
Czy wytłumaczy mi ktoś łopatologicznie skąd wziął się logarytm naturalny, dlaczego jest tak ważny, i dlaczego ma akurat w swojej postawie liczbę e? W chemii fizycznej, termodynamice i przemianach gazu doskonałego, których się własnie uczę pojawia się cały czas... Ale dlaczego? To tylko artefakt matematyczny, czy jakaś rzeczywista wartość związana z fizyką?
Komentarz usunięty przez autora
- 4
#zagadka #matematyka #fizyka
- 4
- 2
Mireczki,może ktoś mi powiedzieć czy dobrze zrobiłem to zadanie? Bo wydaje mi się,że wektory po prawej nie są podobne/zależne liniowo od tych po lewej ( ͡° ʖ̯ ͡°)

źródło: comment_PTQn3bAOGQBwQem28TVznaPtAJdaVcAl.jpg
Pobierz- 33
Na koniec roku trochę humoru naukowego :) Link prowadzi do bardzo ciekawej treści.
To krótkie historie życia słynnych naukowców.
Niektóre obrazki są w języku angielskim, inaczej tracą sens.
Link
![RFpNeFeFiFcL - [ANW] 20 śmiesznych obrazków + anegdoty (i suchary) NAUKOWE
Na koni...](https://wykop.pl/cdn/c3201142/comment_bHkeAtMWyUfIjQq2pPsQW92whLfaYf1g,w400.jpg)
źródło: comment_bHkeAtMWyUfIjQq2pPsQW92whLfaYf1g.jpg
Pobierz- 2
Treść została ukryta...
- 0
31
Szereg Fouriera Animacje Wideo Rozwijania 10...
#matematyka #analiza #całka Wyznaczanie współczynników szeregu Fouriera dla 10 różnych funkcji Mateusz Kowalski\nAutor Wideo Bloga...
z- 0
- #
- #
- #
- #
- #
- #
#wentylacja #budownictwo #matematyka #projektowanie
- 0
- 1
Zrobiłem, ale nie wychodzi, co źle robię?
Prawidłowe odpowiedzi to:
#matematyka #informatyka

źródło: comment_gQZIrFDfLfnpl0cX4v80xCyyRjdBrEwK.jpg
Pobierz52
Scalar - Naukowy kalkulator skryptowy + wykresy dla Android

Scalar to znacznie więcej niż kalkulator. Scalar to potężny silnik matematyczny i język skryptowy, który łączy w sobie prostotę standardowych narzędzi z elastycznością programowania. Dzięki Scalar, definiowanie argumentów i funkcji, a także używanie ich w obliczeniach, nigdy nie było łatwiejsze.
z- 47
- #
- #
- #
- #
- #
- #
- 3
https://gilkalai.wordpress.com/2018/12/25/amazing-karim-adiprasito-proved-the-g-conjecture-for-spheres/
explain like im an undergrad pls
#matematyka
- 1
Wrzucałem już ten filmik, bo wydawał mi się ciekawy ale nie miałem dość czasu aby obejrzeć go do końca. Okazało się, że rysowanie tych kółek nie ma najmniejszego sensu, bo można to bardzo łatwo obliczyć nie zawracając sobie głowy rysunkami.
1/15, 1/23, 1/39, 1/63, ?
Wystarczy

- 0
Skoro "serio nie wiesz po co on je rysował"
Żeby każdy kto to obejrzy zmarnował 26 minut swojego życia (
- 1
- 0
Mamy urnę z 23 kulami oznaczonymi od 1 do 23.
Ciągniemy 3 kule, zapisujemy wynik, zwracamy do urny.
Wykonano 33 próby (czyli łącznie 99 kul), częstość występowania danej kuli przedstawia się następująco:
- 1
1) w każdej próbie jest szansa 3/23 że wyciągniemy daną kulę, 33 próby dają wartość oczekiwaną np=33*(3/23)=4,3 (mniej więcej)
2) wariancja w rozkładzie dwumianowym np(1-p) = 33*(3/23)*(20/23) = 3,743, odch. stand. = 1,935
3) wartość oczekiwana + 3 sigmy: 4,3+1,935 * 3=10,105
wniosek: szansa na osiągnięcie takiego wyniku przy "równych" kulach jest b.mała.
- 0

źródło: comment_l0cFgA4G1I4yoMcXPk2MAg5lhOtlBL8a.jpg
Pobierz- 2
@Edit: Ten plusik to oczywiście różnica symetryczna ^^^
- 1

źródło: comment_RjLGdy0GRI0Xs2WYnHUrNkWk6wVzDdvr.jpg
Pobierz1
Czego jest najwięcej we Wszechświecie? Poza ludzką głupotą
Artykuł z dala od #afera
z- 0
- #
- #
- #
- #
- #
- #
W drugim tak samo, zamieniasz sin5x na coś zależnego od sinx i cosx
- 1
1
Czy na pewno umiesz liczyć pieniądze?

O liczeniu pieniędzy - na wesoło i na poważnie.
z- 0
- #
- #
- #
- #
26
Galileusz i Torricelli: krzywe balistyczne
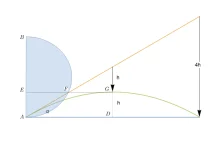
Rewolucja naukowa XVII w. ukazała nowe zastosowania matematyki: poznano kształt orbit planetarnych, a także krzywą balistyczną – tor wystrzelonego bądź rzuconego ciała. Odkrycie parabolicznego kształtu krzywej balistycznej jest jednym ze sławnych osiągnięć Galileusza...
z- 1
- #
- #
- #
- #
- #
- #







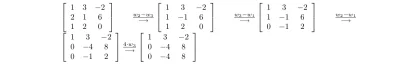



















#matematyka