Wszystko
Najnowsze
Archiwum
59
Jak Archimedes pole koła policzył
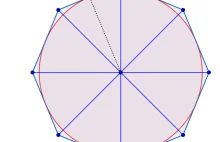
Pole koła policzyć umiał już grecki matematyk, fizyk i inżynier Archimedes (ok. 287–212 p.n.e.). Choć nie do końca jego wynik jest tym co znamy ze szkoły. W tym wpisie przedstawiony został zaadaptowany do dzisiejszych czasów dowód Archimedesa.
z- 1
- #
- #
- #
- #
- #
- #
14
Jak poprawnie rysować cienie? - (reupload bo zdjęli)

Przyspieszony kurs rysowania cieni różnych figur.
z- 3
- #
- #
- #
- #
- #
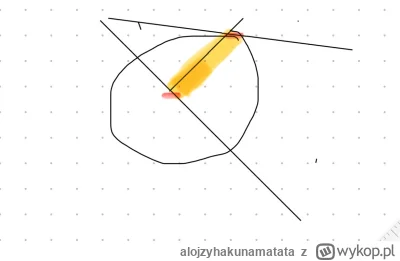
źródło: Zdjęcie z biblioteki
Pobierzwykreśl prostą równoległą do tej prostej na górze, odległą od niej o 12. znajdź jej punkt przecięcia z drugą prostą. tam jest środek okręgu
@alojzyhakunamatata
- 0

źródło: AdobeStock_2186932273
Pobierz- 0

źródło: 12345678369123456789121c
PobierzZbliżenie na diodę świecącej 5 mm (czerwoną) i w komentarzu rozrysowania siatka rozchodzących się refleksów świetlnych.

źródło: 20210223_203331
Pobierz- 4

źródło: 20210223_203331_1
PobierzGeometria, geometria i raz jeszcze geometria. Lubię to!
Miłej niedzieli życzę i pozdrawiam
(Pudełko specjalnie do tego projektu wykonała @Apaturia. Serdecznie pozdrawiam)
#mishmashstudio666
#

źródło: InShot_20231118_230905110
Pobierzhttps://pl.wikipedia.org/wiki/Vesica_piscis
Źródło: Wikipedia
źródło: SPDC_figure
Pobierz16
Dwa tysiące lat historii geometrii.

Ostatni z pięciu aksjomatów Euklidesa, o sumie kątów trójkąta równie 180°, doprowadził do największej rewolucji w historii matematyki naszych czasów.
z- 0
- #
- #
- #
- #
- #
- #
Serio kuhde, nawet rachunek różniczkowy po latach jest jak dla mnie łatwiej na luzie wykminić - niż te potęgi funkcji trygonometrycznych, czy inne pierwiastki z cotangensów, no i jeszcze to do wykresu odnieść...
20
Po co dzbanecznikom wymyślne kołnierzyki? Odpowiedzieli matematycy

Do tej pory opisano 183 gatunki dzbanecznika. Różnią się one między sobą m.in. kształtem pułapek. Są większe i mniejsze. Wąskie i rozdęte. Wiszące wśród drzew i zagłębione w mchu na dnie lasu. Ich brzeg, zwany kołnierzykiem, bywa gładki, rozkloszowany, szeroki i płaski albo pokryty ząbkami...
z- 2
- #
- #
- #
- #
- #
- #
2
Katedry gotyckie, Wielka Piramida i zapach róży - PODCAST #4 - Antoni Ruszkiewic

Czym jest Święta Geometria? Jak starożytne cywilizacje doszukiwały się kodów stworzenia? Zapisy geometryczne w słynnych budowlach. Przebudzenie kundalini. Matematyka jest kodem Boga :)
z- 0
- #
- #
- #
- #
- #
- #
8
Jak Sześcian Neckera pozwala zrozumieć 4D [ENG]
![Jak Sześcian Neckera pozwala zrozumieć 4D [ENG]](https://wykop.pl/cdn/c3397993/b478679c9d4378e02fe700b5cb4c5eb1c8944edaa8882b9e488f171adc0c166b,w220h142.jpg)
Krótki filmik o tym, jak Sześcian Neckera pozwala nam zrozumieć wyższy wymiar przestrzeni.
z- 1
- #
- #
- #
- #
- #
Poznaj brachistochronę.
#ciekawostki #gruparatowaniapoziomu #geometria #matematyka #nauka #gif #infografika
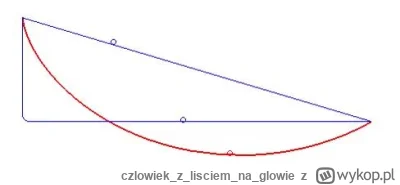
Brachistochrona to krzywa najkrótszego spadku, a nie najmniejsza odległość między punktami.

źródło: tumblr_nl0mwxYOJn1slrk0zo3_500
Pobierz466
Animation vs. Math
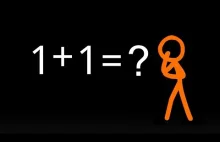
- 36
- #
- #
- #
- #
- #
Członek mojej rodziny ma ponad 90 lat i poważne problemy ze wzrokiem - nie widzi na jedno oko, a na drugie bardzo słabo, tak, że jest w stanie przeczytać tylko większe litery (czcionka o rozmiarze 40-50?) i rozpoznać większe kształty. Ma duże problemy z poruszaniem się, mieszka sam, jest codziennie odwiedzany przez swojego syna. Jednocześnie posiada bystry, matematyczny umysł, który uwielbia ćwiczyć, rozwiązując zadawane samemu sobie zagadki matematyczne,

źródło: canyon-senior-gps-smartwatch-refurbished
Pobierzhttps://allegro.pl/oferta/opaska-dla-seniora-polska-aplikacja-sos-gsm-sim-10467551465?bi_s=ads&bi_m=productlisting:desktop:query&bi_c=ODI3NWNhMjMtZjE3MC00YWE1LTk2OWEtNGNhZjE5MzkwOTJkAA&bi_t=ape&referrer=proxy&emission_unit_id=da5718d9-0934-4416-98ed-84766cc2231a
12
Parabola również ma swoje "π"
To, że stosunek obwodu koła (czyli długości okręgu) do długości jego średnicy jest zawsze równy π wynika z tego, że wszystkie okręgi są do siebie podobne. Podobnie sytuacja wygląda z parabolami. W jaki sposób otrzymać stałą paraboliczną?
z- 3
- #
- #
- #
- #
- #
- #
13
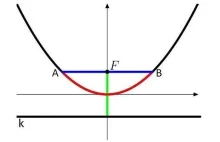
Co łączy żarłoczną kozę i całki zespolone?
Problem określany jest najczęściej zadaniem z kozą bądź geometrycznym problemem kozy, ale występuje również pod innymi podobnymi nazwami. Pomimo długiej historii rozwiązanie go jawnym wzorem ukazało się dopiero w 2020 r. Jest na tyle ciekawe i zaskakująco sprytne, że warto mu się bliżej przyjrzeć.
z- 0
- #
- #
- #
- #
- #
- #
639
Matematycy odkryli nowy kształt o niezwykłych właściwościach. Czapki z głów

Po ponad 50 latach poszukiwań, naukowcy znaleźli świętego Graala figur geometrycznych. "Einstein" to jeden kształt, który sam może pokryć dowolną płaszczyznę bez powtarzania wzoru.
z- 125
- #
- #
- #
- #
- #














https://www.facebook.com/share/r/5P5wFBz5BJyBCrg6/
#matematyka #geometria #ciekawostki
Podobnie z Ziemią która w ciągu roku robi 366,24 obrotów wokół własnej osi (a dni jest przecież 365,24). Jeden dodatkowy obrót pochodzi od obrotu wokół słońca.
Masz wyjaśnienie na 10 stronie:
https://www.geografia24.eu/geo_prezentacje_pp_1/351_2_ziemia_we_wszechswiecie/pp1_2_03a.pdf