Matematycy odkryli nowy kształt o niezwykłych właściwościach. Czapki z głów

Po ponad 50 latach poszukiwań, naukowcy znaleźli świętego Graala figur geometrycznych. "Einstein" to jeden kształt, który sam może pokryć dowolną płaszczyznę bez powtarzania wzoru.

[kamehameha]

Nowy trend płytkarsko-łazienkowy 3,2,1...

[KrowaDajeMleko]

@kamehameha: weź nawet nie mów tak zbyt głośno, już widzę fugowanie tego XD

[autotldr]

To najlepszy tl;dr, jaki mogłem zrobić, oryginał zmniejszony o 67% (jestem botem)

Aperiodyczy monotyl, znany również jako „einstein” – nie od nazwiska austriackiego fizyka, a niemieckiego wyrażenia oznaczającego jeden kamień (ein stein) – to kształt poszukiwany przez matematyków od dawna.

Mowa o jednej figurze, która jest w stanie zapełnić dowolną powierzchnię w unikalny (aperiodyczny) sposób.

Nie było pewności, że einstein istnieje, ale udało się go namierzyć dzięki modelowaniu komputerowemu.

Powstał on jednak

[Rabusek]

@autotldr: za co te minusy Ty dostajesz, kolejny klik mniej dzieki podsumowanku

[bialy100k]

@Rabusek: Zapewne za marne TL;DR które używa wyrwanych z kontekstu zdań.

Np: "kapelusze układają się w większe skupiska" z TL;DR nie mówi nic sensownego, dopóki nie wiemy, że figura to:
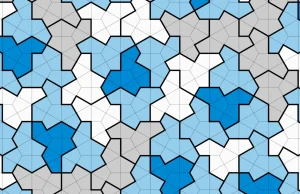
13-boczny kształt, nazywany także “kapeluszem”

Jak na razie ludzie potrafią syntetyzować informacje czytelniej.

[Tym]

Zabrakło jednego, poważnego zastrzeżenia. Ten kształt faktycznie pozwala pokryć całą powierzchnię, ale pod warunkiem, że mniej więcej co 4. kafelek będzie odwrócony "do góry nogami". Zatem w wymiarze praktycznym, żeby wykafelkować tym łazienkę trzeba by mieć nadal 2 rodzaje kafelków "lewe" i "prawe".

Na grafice poniżej te żółte kafelki to te "odwrócone":

[Kinda]

@Titsuman chodzi o to że wzór w przypadku kwadratów będzie powtarzalny, a w przypadku tego kształtu nie powtórzy się nigdy niezależnie jak dużą powierzchnię nim pokryjesz.

[s.....e]

@Tym: przyklei się tył na przód i nikt nie zauwazy

[krzywy_odcinek]

W końcu koniec z największą zmorą w grach ( ͡° ͜ʖ ͡°)

[zapomnialemhaslo]

@krzywy_odcinek: ciekawe ile mocy obliczeniowej wiecej bedzie potrzebne zeby uzyc takich ksztaltow

[jaqjaq]

@krzywy_odcinek:
Po pierwsze, problem ten został rozwiązany wielokrotnie w przeszłości na różne sposoby.
Po drugie, ten wzór nie jest powtarzalny z matematycznego punktu widzenia, ale nasz mózg widzi jego powtarzalność, więc zastosowanie go do teksturowania nie ma najmniejszego sensu.
Po trzecie, 2005 był dawno temu, a nowe gry posiadają taką ilość mniejszych detali, taką rozdzielczość tekstur i taką ilość różnorakich map nałożonych na siebie, że powtarzalność bazowej tekstury pod spodem nie

[tomilipin]

kamuflarzu

@FFFFUUUU kamuflażu

[h4nter]

@bongos112: temat nie jest nowy. A przydaje się w praktyce, np. jakiś producent papieru toaletowego używa takiej formatki do tłoczenia wzorków na papierze. Dzięki temu przy nawijaniu na rolkę papieru będzie optycznie więcej, bo wzorki na siebie się nie nakładają. Przy powtarzalnych wzorach, papier się samoczynnie kompresuje, bo warstwy się na siebie nakładają. Przy tym algorytmie żadna warstwa papieru na rolce nie będzie ze sobą kompatybilna.

Można tę właściwość wykorzystać do

[chlopiec_kucyk]

„einstein” – nie od nazwiska austriackiego fizyka, a niemieckiego wyrażenia oznaczającego jeden kamień (ein stein)

Ta, na pewno

[ZACIENTY_CAPSLOCK]

@chlopiec_kucyk:

panie... najpierw nazwaliśmy ten wzór Einstein, a dopiero potem się okazało że taki ktoś to był

[guilmonn]

@ZACIENTY_CAPSLOCK: na dodatek większosc ludzi nie wie za co Einstein dostał nobla albo by odpowiedziała źle ( ͡º ͜ʖ͡º)

[Soothsayer]

absolutnie nic nie zrozumiałem

[benzene]

Duże powierzchnie najlepiej pokryć gładzią szpachlową. Wtedy także nie powtarza się wzór. I jest elegancko.

[RandomowyMirek]

@benzene:
Ja bym tam zrobił na karton gips....

[kar-tofel]

@uzytkownik2560: Tutaj sie nie zgodze, metoda ta jest wynalazkie brytow.( ͡º ͜ʖ͡º)

[MrCreosote]

Matematycy odkryli nowy kształt

Nie "matematycy" tylko drukarz. David Smith jest emerytowanym drukarzem, miłośnikiem puzzli. Swoje odkrycie pokazał matematykowi, Craigowi Kaplanowi, żeby ten potwierdził czy faktycznie udało mu się odkryć einsteina.

[IroL]

50 lat poszukiwań i będą płytki nowego kształtu, no #!$%@? by strzelił.

[killuawykop]

@IroL: ale może też multimetylowe ultrakryształy* posiadające unikalne właściwości :)
PS: *wymyśliłem z różnych słów z artykułu)