Df funkcji lnx/ctgx to ] 0 ; pi/2 [ ? #pytanie #matematyka
@Brun0: zdecydowanie nie, ogarnij się, przecież to w ogóle nie pasuje.
Wszystko
Najlepsze
Archiwum
Odkryto kolejną, największą liczbę pierwszą - ma 17 milionów cyfr
- 121
- #
- #
- #
- #
- #
Jak ktoś lubi #humor w stylu #bash czy #roflcopter to polecam zbiór cytatów wykładowców z Polibudy: KLIK.
Spędziłem dobre pół godzinki na lekturze tych cytatów, humor skutecznie poprawiony mimo egzaminu za 8h :)
#informatyka #matematyka #it #geek #nerd
#mikroreklama
Spędziłem dobre pół godzinki na lekturze tych cytatów, humor skutecznie poprawiony mimo egzaminu za 8h :)
#informatyka #matematyka #it #geek #nerd
#mikroreklama
@Bimbermaeister: dziwisz się? Bash powstał dawnooo temu kiedy jeszcze gimbusy nie miały dostępu do sieci. Z czasem coraz większa liczba osób miała dostęp do neta przez co bash przestał być taki hmm nie wiem jak to nazwa... niszowy/chermetyczny
Cytaty wykładowców Politechniki
- 11
- #
- #
- #
- #
- #
- #
- #
Ej, mam w treści zadania o "problemie zanurzania grafu (z dylatacją 1)" - wiem czym jest zanurzanie grafu, ale za cholery nie mam pojęcia o co chodzi z tą dylatacją, ktoś wie? Sprawdzałem w google, ale wiadomo, że jak na 1. stronie czegoś nie ma, to to nie istnieje. #grafy #matematyka #teoriagrafow
@Marmite: http://www.sjp.pl/dylatacja :|
Jeszcze dylatacja czasu mi się kojarzy, a tam w definicji będzie coś o różnicach pomiaru.
Jeszcze dylatacja czasu mi się kojarzy, a tam w definicji będzie coś o różnicach pomiaru.
@anonim1133: Sama dylatacja to ja wiem czym jest, ale nie mam pojęcia jaki to ma związek z zanurzaniem grafu (i dlaczego akurat 1 - z późniejszego wyjaśnienia czym właściwie jest to zanurzanie z dylatacją 1:
nie wynika mi
dane są 2 grafy (G,H), G - gość, H - gospodarz. Czy istnieje odwzorowanie wierzchołków f: V(G) -> V(H) że każdej krawędzi {u,v} należącej do E(G) odpowiada krawędź {f(u), f(v)} należące do E(H)
nie wynika mi
Krótko o liczbach pierwszych
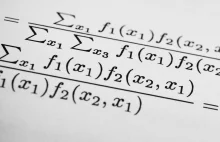
- 41
- #
- #
- #
- #
http://odkrywcy.pl/kat,111408,title,Zagadki-warte-milion-dolarow-kazda,wid,15298241,wiadomosc.html Kocham ten serwis, jest taki idiotyczny. "Zagadki matematyczne" #lolcontent #matematyka
#matematyka #analizamatematyczna Witam. Mógłby mi ktoś wyjaśnić dlaczego x/0 = nieskończoność ?
@JareQ: Nie wiem co to było, ale zapis 6/0=4 jest zupełnie bez sensu.
@JareQ: najlepsze wytłumaczenie, od numberphile: http://www.youtube.com/watch?v=BRRolKTlF6Q
jak obliczyć ekstrema lokalne i przedziały monotoniczności takiego inputa http://www.wolframalpha.com/input/?i=%281%2F2%29^[3x^4-4x^3%2B1] . nie mam pojęcia. ręce opadają, poratuje ktoś? #matematyka global maximum to chyba największa wartość funkcji, a nie o to mi chodzi.
@potoc: help.
F: V1 -> V2. W należy do V1. F(W)(x) = [[(x+1)^2]/2]*W"(x) + (x+1)W'(x).
Pytanie kieruję do studentów kierunków inżynierskich (matematyka w sumie też może być). Umiecie chociażby sprawdzić, czy F jest odwzorowaniem liniowym?
#matematyka #studia
Pytanie kieruję do studentów kierunków inżynierskich (matematyka w sumie też może być). Umiecie chociażby sprawdzić, czy F jest odwzorowaniem liniowym?
#matematyka #studia
#matematyka w jaki sposób liczy się pole figury określonej funkcjami y = -x2 + 1 i y = -x -1 bo część figury znajduje się nad osią X a część pod nią. Oczywiście mowa o całce oznaczonej
Jaka jest najlepsza metoda do obliczania ciągu określonego rekurencyjnie? W ogóle mógłby mi ktoś to wytłumaczyć dokładnie? Bo nie przypominam sobie, żebym miał to w szkole, a jest wymagane na maturze rozszerzonej. #matematyka
@Fheat: nie będzie z tego zadania
Nie mogę rozwiązać : < Jakaś podpowiedź?
http://latex.codecogs.com/gif.latex?\int&space\frac{x^2-1}{x-1}
#pytanie #matematyka #gorzkiezale #buldupy #jestemglupi
http://latex.codecogs.com/gif.latex?\int&space\frac{x^2-1}{x-1}
#pytanie #matematyka #gorzkiezale #buldupy #jestemglupi
nowa jednostka prędkości: ban na godzinę = b/h
w tej chwili wykop mknie z prędkością ok 3b/h
#matematyka #wypok
w tej chwili wykop mknie z prędkością ok 3b/h
#matematyka #wypok
- Endorfinek
- konto usunięte
- konto usunięte
- bejdak
- czuraj
- +5 innych
Profesor z sieci lepszy niż Einstein?
- 161
- #
- #
- #
#matematyka #kiciochpyta
Miał ktoś matematykę na studiach? Pytanie brzmi czy jest jakiś powszechny rozkład podobny do Gausa tylko na przedziale domkniętym od (a, b)?
Miał ktoś matematykę na studiach? Pytanie brzmi czy jest jakiś powszechny rozkład podobny do Gausa tylko na przedziale domkniętym od (a, b)?
wracam z banicji po raz wtóry
pytanie:
Potrzebuję programu który obliczałby prawdopodobieństwo wypadnięcia losowego. Jest pięć pól i na jednym z nich może wypaść. Jak mógłbym obliczyć/przewidzieć prawdopodobieństwo wypadnięcia przy powiedzmy 100 próbach? da rade rozgryźć taki algorytm?
#kiciochpyta #logika #statystyka #matematyka #programowanie #pytanie
pytanie:
Potrzebuję programu który obliczałby prawdopodobieństwo wypadnięcia losowego. Jest pięć pól i na jednym z nich może wypaść. Jak mógłbym obliczyć/przewidzieć prawdopodobieństwo wypadnięcia przy powiedzmy 100 próbach? da rade rozgryźć taki algorytm?
#kiciochpyta #logika #statystyka #matematyka #programowanie #pytanie
@zawszespoko: Na podstawie obserwacji chcesz sprawdzić jak czesto wpada które pole? użyj excela.
funkcja LICZ.JEŻELI oraz wpisywanie w jedną z kolumn znaku odpowiadającego danemu polu.
funkcja LICZ.JEŻELI oraz wpisywanie w jedną z kolumn znaku odpowiadającego danemu polu.
@mariuzpl: ale w jakiej konfiguracji taka funkcja mi pomoże?
Świat matematycznych ignorantów
- 122
- #
- #
- #
- #
Kolejna rzecz do nauczenia się na sesję {:
Komentarz usunięty przez moderatora
Wiecie jaki jest najgłupszy sposób na mnożenie dużych liczby? Właśnie ten:
http://www.youtube.com/watch?v=iHmzmcPSaEA
#matematyka #zdupy #bezsensu
http://www.youtube.com/watch?v=iHmzmcPSaEA
#matematyka #zdupy #bezsensu
@Lukas77986: Na egzaminie tylko hipsterscy-matematycy tak liczą.
@Lukas77986: Jakby się przyjrzeć to to jest dokładnie to samo co nasze dzielenie pisemne "pod kreską", tyle że jak ktoś nie potrafi mnożyć lub dodawać jednocyfrowych liczb to mu łatwiej bo może po kreseczkach policzyć...
Komentarz usunięty przez moderatora
@sens: a gdyby okazało się że któryś poziom cząstek subatomowych nie może zajmować dowolnego miejsca w przestrzeni ale tylko takie, które znajdują się jakby na węzłach siatki. I ruch nie jest ciągły… jak by wtedy wyglądała matematyka?
Mnożenie wektorowe wektorów nie znając cosinusa kąta. Stosując rachunek na macierzach. Ma ktoś link jak to zrobić? :D #pytanie #matematyka #gorzkiezale #wektory
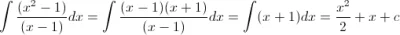
przecież wszyscy już wiedzą, że jesteś facetem, po co się ukrywasz :/