Halko, ogarnia ktoś tu algebrę abstrakcyjną (te podstawowe rzeczy - grupy, monoidy sridy itp.) albo ma jakieś źródło gdzie ładnie jest to wytłumaczone? #studbaza #algebra #matematyka
Wszystko
Najnowsze
Archiwum
@Ni_czas_to_ni_miejsce: spoko, od razu podpowiem, że żaden z tych wektorów nie będzie wektorem własnym https://www.wolframalpha.com/input/?i=Eigenvectors+%7B%7B2,1%7D,%7B8,1%7D%7D
@Ni_czas_to_ni_miejsce: @jaksa0: żeby się nie naliczyć, to można od razu sprawdzić czy te wektory które podali są wektorymi własnymi, tak jak na dole piszesz. Tak jest raczej dużo szybciej.
#algebra #matematyka #studbaza #informatyka
Prowadząc optymalizacje za pomocą twierdzeń algebry Boole'a dochodze do momentu gdy mam
x+x*~y
mam tez chyba pasujace twierdzenie:
Prowadząc optymalizacje za pomocą twierdzeń algebry Boole'a dochodze do momentu gdy mam
x+x*~y
mam tez chyba pasujace twierdzenie:
Dla jakich wartości parametru p należącego do R układ ma niezerowe rozwiązania? Wyznaczyć te rozwiązania.
(1-p)x+2y+z=0
x + (2-p)y+z=0
x+2y+(1-p)z=0
(1-p)x+2y+z=0
x + (2-p)y+z=0
x+2y+(1-p)z=0
Co to znaczy niezerowe rozwiązania, tak właściwie?
@Zacny_Los: zauważ, że dla dowolnego p (x,y,z)=(0,0,0) byłoby rozwiązaniem tego układu równań. To jest zerowe rozwiązanie. Chodzi o to, żeby ustalić dla jakich p układ równań będzie miał też jakieś inne rozwiązania (tzn. niezerowe).
2x+y+2z=0 (p=0) (i co teras?)
@Zacny_Los: Skąd się to wzięło? Jak p=0, to każde równanie w tym układzie równań będzie wyglądało tak samo. Generalnie ważne że jak W się zeruje to wyjdzie układ nieoznaczony, bo w tym zadaniu interesuje cię jedynie to, żeby miał niezerowe rozwiązania, a to już powinieneś wiedzieć.
Mirki mam problem z algebrą...
Mam takie oto zadanie:
Dla jakiej wartości parametru p układ ma rozwiązanie niezerowe
(1-p)x + 3y + 3z = 0
3x + (1-p)y + 3z = 0
3x + 3y + (1-p)z = 0
Mam takie oto zadanie:
Dla jakiej wartości parametru p układ ma rozwiązanie niezerowe
(1-p)x + 3y + 3z = 0
3x + (1-p)y + 3z = 0
3x + 3y + (1-p)z = 0
jest on jednorodny bo rz(A)=rz(A|b) i wyrazy wolne to same 0
@OstryKepucz: układ jest jednorodny gdy wszystkie wyrazy wolne są równe 0, rzędy nie mają tu znaczenia.
rz(A)=rz(A|b)
to jest prawda w jednorodnych, ale w jaki sposób wywnioskowałeś, że rz(A)=rz(A|b) <n=3 ?
@OstryKepucz:
1. ok
2. Układ niejednorodny nigdy nie ma rozwiązania zerowego (co łatwo sprawdzić podstawiając to zerowe rozwiązanie)
1. ok
2. Układ niejednorodny nigdy nie ma rozwiązania zerowego (co łatwo sprawdzić podstawiając to zerowe rozwiązanie)
Które z podanych zbiorów liczbowych wraz ze zwykłymi działaniami dodawania i mnożenia są ciałami:
jakieś pomysły?
#matematyka #algebra
jakieś pomysły?
#matematyka #algebra
źródło: comment_ZFYLUbF97na4xxK3v4br5pjPBBRANNeY.jpg
Pobierz@agsbajahs: Prawie wszystkie te przykłady to ciało kwadratowe Q(sqrt(d)), znane i dość ciekawe ciało, którego szczególnym przypadkiem jest Q(i) czyli tzw. ciało Gaussa: https://en.wikipedia.org/wiki/Quadratic_field
jakieś pomysły?
@agsbajahs:
No trzeba se zobaczyć definicję ciała i zobaczyć czy zbiory spełniają zawarte w niej warunki.
Jak wykazać jednoznaczność rozkładu wektora w ustalonej bazie? #matematyka #studbaza #politechnika #algebra #pytanie
@kuba_kuba: w skrócie: gdyby dało się go rozłożyć na dwa różne sposoby to któryś wektor bazowy musiałby być liniowo zależny od pozostałych
@kuba_kuba: niech V = p. lin nad K, dim V = n, w należy do V, B = baza V, a1,...,an należą do K, z1,...,zn należą do K
jeśli w = a1b1 + a2b2 + ... + anbn i jednocześnie w = z1b1 + z2b2 + ... + znbn to wtedy
w-w = 0 = (a1-z1)b1 + (a2-z2)b2 + ... +
jeśli w = a1b1 + a2b2 + ... + anbn i jednocześnie w = z1b1 + z2b2 + ... + znbn to wtedy
w-w = 0 = (a1-z1)b1 + (a2-z2)b2 + ... +
potrzebuje pomocy w #algebra boole'a - chodzi o Siatkę Karnaugha.
Jak na zdjęciu, mam do optymalizacji i utworzeniu schematu tylko dla bramek NAND funkcję:
F = ∑[4,5,6,8,9,10,13(0,7,15)]
stworzyłem zatem tablicę prawdy (dla 0,7,15 dałem kreskę bo podobno mogę sobie wtedy decydować czy to 1/0 w siatce Karnaugh), następnie zrobiłem ów siatkę i połączyłem grupy. Ze względu na to, że robię to dla NANDów to połączyłem '1' czyli wyszła suma iloczynów. Zoptymalizowałem to
Jak na zdjęciu, mam do optymalizacji i utworzeniu schematu tylko dla bramek NAND funkcję:
F = ∑[4,5,6,8,9,10,13(0,7,15)]
stworzyłem zatem tablicę prawdy (dla 0,7,15 dałem kreskę bo podobno mogę sobie wtedy decydować czy to 1/0 w siatce Karnaugh), następnie zrobiłem ów siatkę i połączyłem grupy. Ze względu na to, że robię to dla NANDów to połączyłem '1' czyli wyszła suma iloczynów. Zoptymalizowałem to
źródło: comment_iW07ysrDyyIjkYIxmSbgi0uo8YrdbhpP.jpg
Pobierz@molibdenowy_wojtek: o fuck, faktycznie, już to sprawdzę
@molibdenowy_wojtek: działa, dziękuję!
w 10 doszedłem do momentu w którym z = 4 - i, teraz muszę policzyć pierwiastki 5 stopnia ale do postaci trygonometrycznej/algebraicznej nie da rady przerobić bo wartości funkcji tryg. są bardzo nieładne. Jak takie coś ugryźć? #matematyka #algebra #liczbyzespolone #pomocy #politechnika
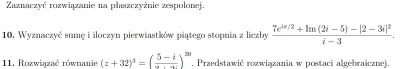
źródło: comment_JFCdeUEMCxwmyqpEUilOqcNDlZo8IX6i.jpg
Pobierz@kuba_kuba: rozważ wielomian z^5 - (liczba z zadania) i skorzystaj ze wzorów Viete https://pl.wikipedia.org/wiki/Wzory_Viète’a
@statoscope: okey dzieki wielkie ;))
Jeżeli macierz A jest macierzą współczynników układu 6 równań o 5 niewiadomych i r(A) = 5,
wtedy rząd macierzy rozszerzonej A|B może być równy:
A. 3
B. 4
C. 5
wtedy rząd macierzy rozszerzonej A|B może być równy:
A. 3
B. 4
C. 5
miałem to dość dawno ale chyba 6, bo dokładając jedną kolumnę nie możemy zmniejszyć liczby liniowo nirzależnych wierszy (nawet jak wpiszemy same 0 to nadal mamy 5 liniowo niezależnych) natomiast mamy 6 równań z czego 5 jest liniowo niezależnych. Dla ustalenia uwagi niech pierwsze 5 będzue liniowo niezależne. Wtedy ostatnie równanie jest liniowo zależne od pozostałych ( x*pierwsze równanie + y* drugie równanie itd). No to teraz wystarczy popatrzeć na kolumnę B
@Szachu:
"Wykłady z algebry liniowej" - T.Koźniewski
https://github.com/wiedzmac/University/blob/master/2014-2015/Lato/Algebra/Ciekawe%20materia%C5%82y/Wyk%C5%82ady%20z%20algebry%20liniowej%20wyd.5%20T.%20Ko%C5%BAniewski.pdf
Nic lepszego nie istnieje
"Wykłady z algebry liniowej" - T.Koźniewski
https://github.com/wiedzmac/University/blob/master/2014-2015/Lato/Algebra/Ciekawe%20materia%C5%82y/Wyk%C5%82ady%20z%20algebry%20liniowej%20wyd.5%20T.%20Ko%C5%BAniewski.pdf
Nic lepszego nie istnieje
@Szachu: Jurlewicz, Skoczylas I i II
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
Co to jest delta i wyróżnik wielomianu? Jaki jest tego sens?
Prawie każdy słyszał o delcie. Niektórzy znają też inną nazwę wyróżnik trójmianu kwadratowego. Nie spotkali się jednak z innymi wyróżnikami, które istnieją np. dla czworomianu sześciennego. W tym miejscu nabiera sensu pytanie dlaczego ten wyróżnik ma właśnie taki wzór a nie inny i co w oznacza.
z- 0
- #
- #
- #
- #
- #
- #
#matematyka #algebra
W tematyce przestrzeni liniowych: czym różni się np. przestrzeń R4 (rzeczywista z indeksem górnym 4) od E4 (euklidesowa i z indeksem górnym 4)? Rozwiązuję zadania z algebry i właśnie nagle zmieniły się oznaczenia przestrzeni liniowych z R na E i zastanawiam się czy ma to jakieś szczególne konsekwencje mające wpływ na poprawność rozwiązań?
W tematyce przestrzeni liniowych: czym różni się np. przestrzeń R4 (rzeczywista z indeksem górnym 4) od E4 (euklidesowa i z indeksem górnym 4)? Rozwiązuję zadania z algebry i właśnie nagle zmieniły się oznaczenia przestrzeni liniowych z R na E i zastanawiam się czy ma to jakieś szczególne konsekwencje mające wpływ na poprawność rozwiązań?
@obserwator_z_prawem_interwencji: Jestem głęboko przekonany że to jeden c--j
@obserwator_z_prawem_interwencji:
E4 będzie miała dołączony iloczyn skalarny
E4 będzie miała dołączony iloczyn skalarny
#matematyka #algebra #agh