Wszystko

Najnowsze

Archiwum

o.....i
o.....i
  • 1
#matematyka #algebra

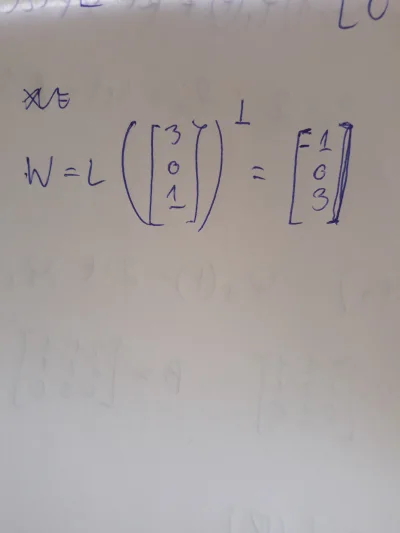
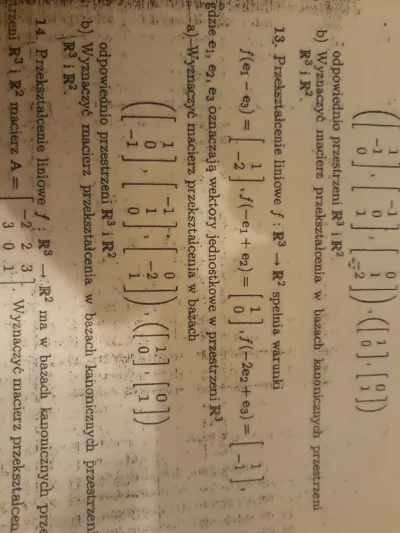
W tematyce przestrzeni liniowych: czym różni się np. przestrzeń R4 (rzeczywista z indeksem górnym 4) od E4 (euklidesowa i z indeksem górnym 4)? Rozwiązuję zadania z algebry i właśnie nagle zmieniły się oznaczenia przestrzeni liniowych z R na E i zastanawiam się czy ma to jakieś szczególne konsekwencje mające wpływ na poprawność rozwiązań?
  • 2
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
C.....c
C.....c
  • 2
Mireczki i Mirabeleczki, jaka książka do #matematyka wyższa, tak dla siebie, do poczytania, dokształcenia się. Poziom #studia #studbaza i wyżej.
Co bym chciał najbardziej? Całeczki, pochodne, gradienty, rotacje, dywergencje, macierze, płaszczyzny różnego rodzaju, #statystyka, #prawdopodobienstwo, #analiza, #algebra, matematykę dyskretną.
Podejrzewam, że jedna książka tego dobrze nie ogarnie, więc słucham propozycji.
  • 22
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
tyrytyty
  • 2
@Cooltec: może zamiast analizy wstęp do teorii mnogości? IMO jeśli nie będziesz z tego egzaminowany to jest strasznie ciekawe do czytania, np. Wykłady ze wstępu do matematyki Guzicki/Zakrzewski
  • Odpowiedz
kamilspl
  • 1
#matematyka #algebra Jest ktoś w stanie pomóc mi z zadaniem w załączniku?
Wstępnie po rozdzieleniu względem potęg X wyszło coś w stylu [x^2 x^1 x^0]*[4 3 0; -1 -1 1; 3 1 4]*[a;b;c] (notacja matlaba).
Wygląda na to że przekształcenie odwrotne będzie miało postać [-5 -12 3; 7 16 -4; 2 5 -1]. Tylko że nie mam żadnej pewności że to co robię ma sens. I dlaczego argument
kamilspl - #matematyka #algebra Jest ktoś w stanie pomóc mi z zadaniem w załączniku? ...

źródło: comment_PxHZHtcrM5fyYbKkvyPWWYYm2ceOmAGp.jpg

Pobierz
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
leoha
  • 1
Na początku zaznaczę, że z algebrą już dawno nie miałem styczności, więc mogę gdzieś popełnić łatwy błąd.
Problem mam taki, że próbuję wyznaczyć wszystkie elementy ciała skończonego GF(2^8). I teraz tak jak użyję wielomianu (w notacji binarnej będę zapisywał, bo jestem związany z #programowanie i mi łatwiej to czytać, a zapis krótszy) p1=100011011 (czyli x^8+x^4+x^3+x+1) to mi się nie udaje, a jak użyję p2=100011101 to wszystko jest ok. Z tego co
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
koostosh
  • 1
@lizardking_21: oryginalna przestrzeń to prosta, ortogonalna do niej będzie płaszczyzna. Musisz znaleźć dwa liniowo niezależne wektory prostopadłe do tej prostej, przestrzeń rozpięta przez nie to to czego szukasz
  • Odpowiedz
koostosh
  • 1
@liquidph: równanie prostej l jest proste do znalezienia, po prostu są to punkty które spełniają oba równania płaszczyzn. Bierzesz te dwa równania traktujesz jak układ i rozwiązujesz.
  • Odpowiedz
koostosh
  • 2
@liquidph: natomiast pierwsza część robisz tak, znajdujesz wektory normalne do tych dwóch płaszczyzn (1,3,-4),(1,-3,2). Znajdujesz płaszczyznę która zawiera te dwa wektory i przesuwasz ją o stałą tak żeby zawierała punkt zadany
  • Odpowiedz
piotrek-5
piotrek-5
  • 1
#matematyka #algebra
Chcę obliczyć równania ogólne i parametryczne płaszczyzny. Przechodzi ona przez punkt P(2,1,-1) i ma wektor normalny n=(1,-2,3)

Wyliczyłem równanie ogólne: x-2y+3z-7=0. Żeby obliczyć równanie parametryczne, muszę znać dwa wektory rozpinające płaszczyznę. Początkowo myślałem, że żeby znaleźć te wektory, wystarczy znaleźć dowolne zmienne x, y, z pasujące do rówania ogólnego (np. (0, -2, 1) czy (7, 0, 0)). Z tym, że iloraz skalarny każdego z tych
  • 5
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
w.....a
w.....a
  • 1
@piotrek-5:
Tak, wystarczy aby nie były liniowo zależne -> w przypadku 2 aby jeden nie był wielokrotnością drugiego.
Pierwsze dwie współrzędne po prostu strzelasz. Dlaczego? Bo dwa wektory rozpinające mogą być dowolne (byleby należały do płaszczyzny i były lnz). Mogą być prostopadłe do siebie, a mogą nie, da się je wybrać na nieskończoność sposobów.
  • Odpowiedz
James0n
  • 1
Macierz przekształcenia liniowego. Zmiana bazy.

Hej czy byłby ktoś w stanie sposób rozwiązywania takich zadań?

Przyjmując, że A jest macierzą liniowego przekształcenia F w S. Znajdź macierz B liniowego przekształcenia F w R.

A
  • 3
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
James0n
  • 3
Znajdź Ker F (jądro), Im F (obraz), rank F (rząd) oraz zerowość dla podanego przekształcenia
liniowego F: U→V

U=V=R , F(x,y,z)=(x+y,x+y,x+2y−z)

Z definicji ker F = {(x,y,z)∊R^3: F(x) = 0}
  • 9
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
James0n
  • 1
@tyrytyty: A co do zerowości to jest to z definicji:
The nullity of a linear mapping is defined to be the dimension of its kernel (or null space).
Więc w tym przypadku nullityF = 1 ?
  • Odpowiedz
JakTamCoTam
  • 2
@Czimchik: Prawda jest taka, że aby zrozumieć na prawdę co się dzieje na matematyce to musiałbyś ją studiować. Biorąc takie studia na serio, potrzeba niemałego wysiłku intelektualnego. Powiedziałbym, że uprawianie matematyki teoretycznej to już bardziej filozofia. Umiejętności mechaniczne, typu liczenie pozwalają Ci tylko na swobodne poruszanie się w jej wymiarze. Co do pytania, oto definicja z wikipedii oraz wytłumaczenie niektórych pojęć potrzebnych do zrozumienia tegoż zagadnienia:

Wyznacznik – funkcja przyporządkowująca
  • Odpowiedz
James0n
  • 1
Żeby wykazać niezależność musze pokazać, że gdy
ax^2 + b2^x + c*cosx = 0
To a=b=c=0
Więc trzeba podstawić kilka "iksów" i sprawdzić co z tego będzie prawda?
Podstawiłem x = 0 bo wtedy mam ładnego cosinusa i otrzymałem b+c = 0
I co dalej? Nie widzę żadnych 'korzystnych' iksów do podstawienia :/
#matematyka #studia #studbaza #algebra
James0n - Żeby wykazać niezależność musze pokazać, że gdy ax^2 + b2^x + c*cosx = 0 ...

źródło: comment_s0G3rvBJ5Xq4sYiwil8sGpxVWGqwYzuC.jpg

Pobierz
  • 8
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
James0n
  • 3
Ktoś tutaj daje może jakieś korki z algebry w Warszawie XD? Bo jestem na 1. roku studiów i nie do końca ją ogarniam.
->liczby zespolone
->ciała
->grupy
->przestrzenie wektorowe
->przekształcenia liniowe
  • 7
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
r.....s
r.....s
  • 1
@unwiw: tak po prostu i bedzie git? Bo dzisiaj(tydzien temu jak pisalem) stracilem 20% na kolosie z algebry bo jednego gowna nie wymnozylem do najprostszej postaci,a w drugim nie zapisalem wyniku tak jak sobie zyczy prowadzacy ehhhh

to po lewo co sie dzieli przez z zawsze daje granice w nieskonczonosci rowna 0 a to po lewo sie odejmuje wiec fakt xD
  • Odpowiedz
Polewik
  • 3
Mam zadanie, które mnie rozłożyło na łopatki.
Rozwiąż w liczbach całkowitych tenże układ równań:
x+y=667
[x,y]/(x,y)=120
Jakieś pomysły od czego mam w ogóle tutaj zacząc? Bo nie mogę znaleźć żadnego punktu zaczepienia (╯︵╰,)
[x,y] to nww, (x,y) to nwd
#matematyka #algebra
  • 8
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
xvovx
  • 4
jak na ironię najwięcej osób ma z tym problem


@Polewik:

Jak można mieć problem z algorytmem Euklidesa? Przecież to dziecko ogarnie. ( ͡º ͜ʖ͡º)
  • Odpowiedz

Powiązane tagi