Znaleźć wartości i wektory własne macierzy.
Znaleźć elementy macierzowe macierzy A w bazie ich wektorów własnych.
kurłaa o co chodzi z tą drugą częścią o bazie?
#studbaza #algebra #geometria #matematyka
#algebraliniowa
Znaleźć elementy macierzowe macierzy A w bazie ich wektorów własnych.
kurłaa o co chodzi z tą drugą częścią o bazie?
#studbaza #algebra #geometria #matematyka
#algebraliniowa









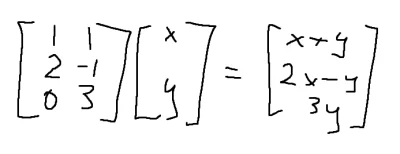












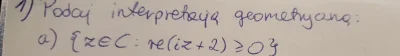



#matematyka #algebra #studia
@Oppaiconnoisseur:
@Chodtok: rozwuj