Wszystko
Najnowsze
Archiwum
478
Zrozumieć liczby zespolone, czyli czym właściwie jest mnożenie

Film ten przedstawia intuicyjne podejście do zagadnienia liczb zespolonych. W prosty sposób umożliwia zrozumienie na pozór skomplikowanych rzeczy przez naucz...
z- 88
- #
- #
- #
- #
- #
#matematyka #liczbyzespolone Czy ktoś ma pomysł jak to rozwiązać ?
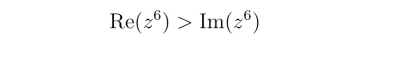
źródło: comment_1581070618RdE5t1XMuyEU6FGeROdctp.jpg
Pobierz@Gggee123: jak się zapisze z = |z|exp(i*\phi), gdzie \phi = arg(z), to idzie
zostajesz z nierównością r^6 cos(6\phi) > r^6 sin(6\phi), bo jak weźmiesz Im, to i Ci znika. Potem możesz dla r!=0 podzielić sobie przez r^6 i dostajesz cos(6\phi)>sin(6\phi) - to już jest zwykła nierówność trygonometryczna
#liczbyzespolone #matematyka #elektronika
Rozpisze ktoś te przejście? próbowałem z zamiany na postać wykładniczą ale wychodzi mi coś innego.
Rozpisze ktoś te przejście? próbowałem z zamiany na postać wykładniczą ale wychodzi mi coś innego.
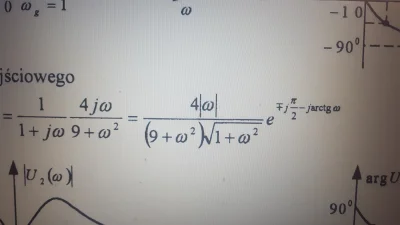
źródło: comment_0CPWBhhiW0nUiH3w3cmy7fMfwHCmtywG.jpg
Pobierz@zamaskowanyszachista: to jest dosłownie z postaci wykładniczej, weź moduł z tego po lewej, a następnie argument. |z|*exp(arg(z)) i to jest Twój wynik, musisz po prostu robić gdzieś błąd
- 0
@tyokke: dzięki, wyszło.
w 10 doszedłem do momentu w którym z = 4 - i, teraz muszę policzyć pierwiastki 5 stopnia ale do postaci trygonometrycznej/algebraicznej nie da rady przerobić bo wartości funkcji tryg. są bardzo nieładne. Jak takie coś ugryźć? #matematyka #algebra #liczbyzespolone #pomocy #politechnika
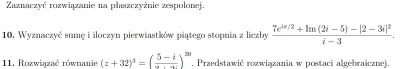
źródło: comment_JFCdeUEMCxwmyqpEUilOqcNDlZo8IX6i.jpg
Pobierz@kuba_kuba: rozważ wielomian z^5 - (liczba z zadania) i skorzystaj ze wzorów Viete https://pl.wikipedia.org/wiki/Wzory_Viète’a
- 0
@statoscope: okey dzieki wielkie ;))
#matematyka #liczbyzespolone
Mam równanie:
Mam zaznaczyć zbiór rozwiązań na płaszczyźnie zespolonej.
Mam równanie:
|z+2|=|z-5+i|Mam zaznaczyć zbiór rozwiązań na płaszczyźnie zespolonej.
- 2
@Winkey: Nie wiesz może dlaczego WolframAlpha podaje jako wynik tego równania jedną liczbę, mianowicie
z=11/7? Moim zdaniem twoje rozwiązanie ma sens, ale skąd w takim razie ta różnica w wynikach?- 2
@piotrek-5: Liczba 11/7 jest jedynym rzeczywistym rozwiązaniem tego równania,
może musisz jakoś zaznaczyć że z należy do zespolonych
może musisz jakoś zaznaczyć że z należy do zespolonych
- 3
W liczbach zespolonych, gdzie mamy z=(x+yi) może mi wyjść na przykład x=2i, czy i musi być z igrekiem, a rozwiązanie jest nieprawidłowe?
#matematyka #kiciochpyta #liczbyzespolone
#matematyka #kiciochpyta #liczbyzespolone
@kozaqu: użyj interpretacji geometrycznej.
- 2
Treść przeznaczona dla osób powyżej 18 roku życia...
- 1
@deryt: Zapomniałeś o drugim pierwiastku, tj. o (-1-i) * sqrt(2)/2
@Pavello: Mi się wygodnie się na to patrzy wizualizując sobie to na płaszczyźnie zespolonej. Wiadomo, że podnoszenie liczby zespolonej do kwadratu podwaja jej kąt a moduł się podnosi do kwadratu. W związku z tym wiadomo, że szukając pierwiastka z i (moduł 1 i kąt 90 stopni) będziemy chcieli czegoś, co będzie miało moduł jeden i kąt 45 stopni
@Pavello: Mi się wygodnie się na to patrzy wizualizując sobie to na płaszczyźnie zespolonej. Wiadomo, że podnoszenie liczby zespolonej do kwadratu podwaja jej kąt a moduł się podnosi do kwadratu. W związku z tym wiadomo, że szukając pierwiastka z i (moduł 1 i kąt 90 stopni) będziemy chcieli czegoś, co będzie miało moduł jeden i kąt 45 stopni
9
Imaginary Numbers Are Real [Part 11: Wandering in 4 Dimensions

Ciekawa seria przybliżająca zagadnienie liczb zespolonych
z- 2
- #
- #
- #
- #
- #
- #
- 1
Jako że zaczęła się sesja a zapał do nauki średni to stwierdziłem, że czemu by nie wrzucać codziennie trochę matematyki. Może mnie to bardziej zmotywuje, a i ktoś skorzysta.
#matematyka #algebra #liczbyzespolone #nejfanmatematykuje #studbaza
#matematyka #algebra #liczbyzespolone #nejfanmatematykuje #studbaza

źródło: comment_zPXBxEYxZVevs68Ljf7OFXHqTW8yiV7Q.jpg
PobierzMirki, pytanie z liczb zespolonych. Jaka jest różnica między arg(z) a arg(4z) w przykładach poniższego typu?
#matematyka #studbaza #liczbyzespolone #algebraliniowa
2pi/3 < arg(4z) <= 11pi/6
#matematyka #studbaza #liczbyzespolone #algebraliniowa
@Tojtek: arg(z) == arg(4z)
Komentarz usunięty przez autora
Pomógłby ktoś z przykładami b, c i d? Z a nie mam problemu, bo łatwo tam porównać so siebie części rzeczywiste i urojone, ale w pozostałych się pogubiłem.
#matematyka #liczbyzespolone #pomusz
#matematyka #liczbyzespolone #pomusz

źródło: comment_tCG0t2QvWrvPUyqaBogIr0zAR2DFY0mG.jpg
Pobierz- 2
Pomógłby ktoś z przykładami b, c i d?
@kocham_jeze: Myślę, że nauczyciel matematyki dałby radę na dyżurze.
- 2
@kocham_jeze: Jaki masz konkretnie problem? Wykorzystujesz to, że
i^2 = -1 do uproszczenia obu stron i to, że x, y należą do R, w ten sposób, że układasz sobie układ równań, taki, że to co przy i (część urojona) po obu stronach równania jest równe i to co bez i (część rzeczywista) po obu stronach równania jest równe. Na przykład dla c:(x + i)(3 - iy) = 1 + 13iMam problem z zadaniem:
wyznaczyć wszystkie z dla których wyrażenie w=z/z+i jest liczbą a)rzeczywistą b) urojoną
#matematyka #liczbyzespolone
wyznaczyć wszystkie z dla których wyrażenie w=z/z+i jest liczbą a)rzeczywistą b) urojoną
#matematyka #liczbyzespolone
- 1
@ludolfina98: z = a + bi
niech z != 0
z / z+i = a+bi /[a+(b+1)i] = 1 - i /[a+(b+1)i] = 1 - [a-(b+1)i]i / |z| = 1 - (b+1) / |z| - i * a / |z|
to jest rzeczywiste gdy a =0
niech z != 0
z / z+i = a+bi /[a+(b+1)i] = 1 - i /[a+(b+1)i] = 1 - [a-(b+1)i]i / |z| = 1 - (b+1) / |z| - i * a / |z|
to jest rzeczywiste gdy a =0
@ludolfina98: a) wyznacz część rzeczywistą i urojoną, a następnie sprawdź kiedy część urojona jest równa zero.
b) Wszystko poza z=-i. Po prostu mianownik nie może się zerować.
b) Wszystko poza z=-i. Po prostu mianownik nie może się zerować.
Mirko, potrzebuje pomocy.
Otóż, jeżeli mam równanie kwadratowe x^2+25 = 0, to delta wychodzi ujemna, więc teoretycznie brak rozwiązań, ale czy można użyć zbioru liczb zespolonych, żeby uzyskać rozwiązanie ? W tym wypadku x=5i v x=-5i, jeżeli dobrze rozumiem?
#licbaza here i nie ma tego w programie, a jestem ciekawy. ( ͡° ͜ʖ ͡°)
#pomocy #matematyka #liczbyzespolone #rownaniakwadratowe
Otóż, jeżeli mam równanie kwadratowe x^2+25 = 0, to delta wychodzi ujemna, więc teoretycznie brak rozwiązań, ale czy można użyć zbioru liczb zespolonych, żeby uzyskać rozwiązanie ? W tym wypadku x=5i v x=-5i, jeżeli dobrze rozumiem?
#licbaza here i nie ma tego w programie, a jestem ciekawy. ( ͡° ͜ʖ ͡°)
#pomocy #matematyka #liczbyzespolone #rownaniakwadratowe
j3 * j3 = (-9) ?
j3 + j3 = (j6) ?
j3 - j3 = (j) ?
j3 / j3 = ?
Mireczki jak to z tymi liczbami zespolonymi?
#matematyka #liczbyzespolone #elektrotechnika #techbaza #elektronika
j3 + j3 = (j6) ?
j3 - j3 = (j) ?
j3 / j3 = ?
Mireczki jak to z tymi liczbami zespolonymi?
#matematyka #liczbyzespolone #elektrotechnika #techbaza #elektronika
Ej mirasy, pytanie z matematyki.
Gdzie leżą na płaszczyźnie zespolonej te liczby z, które spełniają warunek:
|z+1|+|z-1|=3
Bardziej
Gdzie leżą na płaszczyźnie zespolonej te liczby z, które spełniają warunek:
|z+1|+|z-1|=3
Bardziej
- 1
@michalo94: Ja bym rozpisał liczbę zespoloną jako z = x+yi. Następnie zastosowałbym wzór na moduł liczby zespolonej tj. |z| = sqrt(x^2 + y^2). Problem w tym, że wychodzi dalej równanie sqrt((x-1)^2+y^2)+sqrt((x+1)^2+y^2) = 3, a to według Wolframa daje nam elipsę:
http://www.wolframalpha.com/input/?i=sqrt%28%28x-1%29^2%2By^2%29%2Bsqrt%28%28x%2B1%29^2%2By^2%29+%3D+3
http://www.wolframalpha.com/input/?i=sqrt%28%28x-1%29^2%2By^2%29%2Bsqrt%28%28x%2B1%29^2%2By^2%29+%3D+3
- 1
@Szab: Mamy dwa okręgi, jeden o środku w (-1,0), a drugi o środku (1,0). Suma odległości między ich środkami, a jakimś punktem ma być zawsze równa 3, więc chyba się zgadza. Wynikiem będzie ta elipsa. To ma nawet sens. Dzięki ;)
8
Technika kolorowania dziedziny liczb zespolonych
Czyli kiedy klasyczna matematyka to za mało...
z- 1
- #
- #
- #
- #
- 2
@herejon: ale (-1)^2 to Ty się naucz obliczać





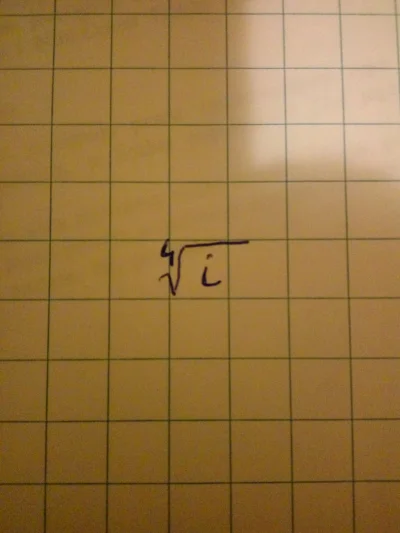

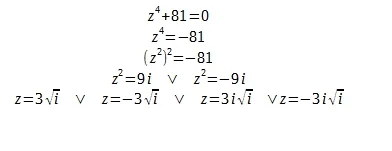















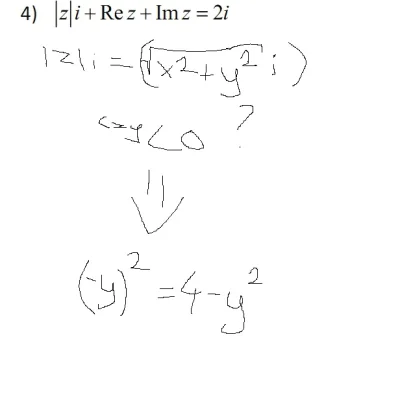
#studbaza #matematyka #liczbyzespolone
źródło: comment_1670176641t63bussDZnsefM3sIc3GHG.jpg
Pobierz