Aktywne Wpisy

klaudia-hadalala +22
Dzisiaj sprzątałem u mamy na strychu. W rogu, za starymi nartami, stała szafa. Ta sama, którą mój ojciec przywiózł na początku lat 90. Nie ruszałem jej od lat. Pamiętałem, że skrywała skarby.
Otworzyłem drzwi i ten zapach. Kurzu, starych gazet i... magii.
• Kasety VHS opisane flamastrem: "Matrix bootleg", "Terminator 2 Polsat", "Wakacje 98". Czasem zastanawiam się, ile razy przewijałem ten "bootleg" ołówkiem, żeby oszczędzić baterie w walkmanie.
• Worek z klockami Lego. Ale nie
Otworzyłem drzwi i ten zapach. Kurzu, starych gazet i... magii.
• Kasety VHS opisane flamastrem: "Matrix bootleg", "Terminator 2 Polsat", "Wakacje 98". Czasem zastanawiam się, ile razy przewijałem ten "bootleg" ołówkiem, żeby oszczędzić baterie w walkmanie.
• Worek z klockami Lego. Ale nie

źródło: IMG_4156
Pobierz
lokomotyva +31
Oglądam skipujac tego gremlina z zatkanym nosem jak materiał komentuje o grach roku.
Polecam ogólnie każdemu zajrzeć aby się upewnić jak bardzo ten człowiek nie ma pojęcia, nie rozumie co w grach jest dobrego i jak bardzo odklejony jest w swoich opiniach.
W wiedźminie to najlepsze co było to gwint oczywiście gdzie ja jako naczelny fan Wieśka który czytał książki kilka razy grę przeszedłem 5 razy na 100% nawet w grze nie tknąłem
Polecam ogólnie każdemu zajrzeć aby się upewnić jak bardzo ten człowiek nie ma pojęcia, nie rozumie co w grach jest dobrego i jak bardzo odklejony jest w swoich opiniach.
W wiedźminie to najlepsze co było to gwint oczywiście gdzie ja jako naczelny fan Wieśka który czytał książki kilka razy grę przeszedłem 5 razy na 100% nawet w grze nie tknąłem

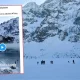



#matematyka
źródło: comment_tUC7R0glpeDaUtYp8NYlUbebNQsm15gy.jpg
Pobierz