Mirki, wytłumaczy mi ktoś ten przykład? skąd się tam wzięło 3^5+2^5?. Tzn. wiem skąd 3 ale nie wiem skąd 2 i ta potęga.
#matematyka #macierze
#matematyka #macierze
Wszystko
Najnowsze
Archiwum
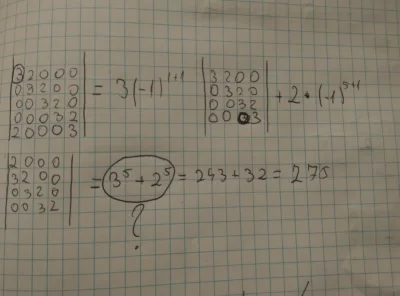
źródło: comment_SOnZhznS7q9hjZFmYw4B6YKh4KaMhL7Q.jpg
Pobierzhttps://play.google.com/store/apps/details?id=net.appassion.dark.matrix.calculator
https://itunes.apple.com/us/app/matrix-calculator/id949123052

źródło: comment_2mDqOs3lVG2DdKzb9MWWzbrOVgztLyeZ.jpg
Pobierz3x+4y = 0, czyli rozwiązanie to: x = 4t, y=-3t, gdzie t jest dowolną liczbą rzeczywistą. Zatem jądro macierzy to: Lin{ (4,-3) }.Komentarz usunięty przez autora

źródło: comment_NvuRnazLrXz4lCVe1aqMDeEFO8aupleI.jpg
Pobierz


źródło: comment_RApa3weGzLzxletGKyaLU3OCUaSYOONK.jpg
PobierzKomentarz usunięty przez moderatora
Wykop.pl
źródło: comment_KkehiuDGhHnmGKVbXVWc8qjrfFDt3ZEz.jpg
PobierzKomentarz usunięty przez autora