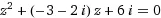#algebra Jest tu ktoś kto ogarnia algebrę? Nie do końca rozumiem końcówki zadania z przekształcenia liniowego.
Wszystko
Najnowsze
Archiwum

Gwozdziuuu
- 1
- 1
Jak sprawdzić czy odwzorowanie liniowe jest epimorfizmem? Czy warunkiem wystarczającym jest to żeby (f: V->W) dla odwzorowania f dim W = dim Im f ? #matematyka #egzamin #algebra #pomoc

ntskj
- 0
@1608: i jak poszło?

1608
- 0
@ntskj: Całkiem nieźle, trochę namieszałem na początku z liczeniem wyznacznika macierzy (tak wiem, najprostsza rzecz ale w stresie człowiek robi różne dziwne rzeczy, w koncu się poprawiłem) ale na szczęście diagonalizacja, relacje i odwzorowania raczej dobrze poszły i wydaje mi się że egzamin zdany :)
Napisz równanie ogólne płaszczyzny przecinającej krawędź przecięcia płaszczyzn
pi1,pi2 i prostopadłej do płaszczyzny pi3.
pi1: x+y-z-3=0 pi2: 2x-y-3z-8=0 pi3: 2x-y+z-6=0
Czy żeby udowodnić, że nie ma elementu odwrotnego dla działania x wystarczy podstawić pod a, do działania
a x a^-1 = a^-1 x e
jakąś liczbę która go nie spełnia? #algebra #matematyka
a x a^-1 = a^-1 x e
jakąś liczbę która go nie spełnia? #algebra #matematyka
@duffman:
1. "element odwrotny do innego elementu względem działania"
2. Definicja: b jest elementem odwrotnym do a względem działania x <=> a x b = b x a = e
3. Jeśli chcesz udowodnić, że w danym zbiorze nie każdy element ma element odwrotny względem działania x, to wystarczy wskazać w nim element, który nie ma elementu odwrotnego w tym zbiorze.
1. "element odwrotny do innego elementu względem działania"
2. Definicja: b jest elementem odwrotnym do a względem działania x <=> a x b = b x a = e
3. Jeśli chcesz udowodnić, że w danym zbiorze nie każdy element ma element odwrotny względem działania x, to wystarczy wskazać w nim element, który nie ma elementu odwrotnego w tym zbiorze.
- 0
Mam działanie a o b =a^b w zbiorze liczb naturalnych i mam sprawdzić co za struktura. Jak sprawdzić czy jest łączne?
Mam takie coś:
( a o b ) o c = a o ( b o c )
L
Mam takie coś:
( a o b ) o c = a o ( b o c )
L
Macie jakieś materiały, z których w 24h nauczę się wszystkiego o strukturach algebraicznych do pierścieni włącznie? #matematyka #algebra #niezdam
@duffman: http://home.agh.edu.pl/~gora/algebra/Wyklad02.pdf + książka skoczylasa z teorią i zadaniami. Wystarczy, cudów Ci pewnie nie trzeba.
#matematyka #algebra #studbaza
Jak wyliczyć macierz przejścia z bazy Alfa do bazy Beta? Mam sprzeczne informacje i już się pogubiłem.
Jak wyliczyć macierz przejścia z bazy Alfa do bazy Beta? Mam sprzeczne informacje i już się pogubiłem.
@jestempirat: (#) Kolumny tej macierzy to wektory nowej bazy zapisane w bazie starej.
- 0
Spójrzcie Mirasy w czym mam problem: http://www.matematyka.pl/355531.htm
- 1
Niech, któryś mirek zerknie czy dobrze robię:
x, a, b, c - macierze
a * x^-1 * b = c
Czy
x, a, b, c - macierze
a * x^-1 * b = c
Czy
- 1
#matematyka #algebra ile jest homomorfizmów pomiędzy z16 a z8? 16?
- 1
jeżeli wyznacznik macierzy jest równy wyznacznikowi macierzy transponowanej, to znaczy że mogę sobie wyciągać stałe(skalary ( ͡° ͜ʖ ͡°)) z wierszy bez żadnych konsekwencji? #matematyka #algebra #pytaniematematyczne
- 1
@merqn: No obstawiałbym coś takiego, ale ja uczyłem się tych rzeczy jeszcze w zeszłym tysiącleciu... W sumie nie wiem czy w definicji grupy jest napisane, że musi posiadać jakikolwiek element niezerowy. wtedy {0,+} też dawałoby radę.
- 2
@merqn {0,+} jest najmniejszą grupą i jednocześnie najmniejszą grupą abelową (przemienną).
- 0
@dudek2: gratuluje profesora :D
- 0
@tangerine_: macierze tak, dowody nie ;)
@DreamyOfficialMusic: wzor skroconego mnozenia?
(a^2+b^2)^2 daje ci dodatkowe skladniki, ktore musisz odjac by sie zgadzalo z lewa strona
(a^2+b^2)^2 daje ci dodatkowe skladniki, ktore musisz odjac by sie zgadzalo z lewa strona
- 0
@Vorland: ok, rozumiem, dzieki:)
- 1
#matematyka #algebra jaki bedzie wyznacznik takiej macierzy:
| logaB 1 |
| 1 logbA |
1 logarytm przy podstawie A z liczby B a drugi odwrotnie. Pomozecie?
| logaB 1 |
| 1 logbA |
1 logarytm przy podstawie A z liczby B a drugi odwrotnie. Pomozecie?
Treść przeznaczona dla osób powyżej 18 roku życia...
- 1
Mam relacje: (obrazek)
Dla k należących do naturalnych dodatnich. Dla k = 7 podaj:
[2]=?
[5]=?
Dla k należących do naturalnych dodatnich. Dla k = 7 podaj:
[2]=?
[5]=?

źródło: comment_6UhGzNirXmNop5X8sXJLizqkLRXBtf8I.jpg
Pobierz- 4
@1608: k ma dzielić bez reszty różnicę m i n. Zatem klasa abstrakcji [2] będzie się składać z takich liczb, że (2-m)=7x dla dowolnej liczby całkowitej x. A więc na przykład -5, 2, 9, 16 (już chyba widzisz schemat).
- 2
@1608: RELACJE

źródło: comment_Pe5hCb8p1ZyQ0V8rdSmGNtlD3l5uyCqx.jpg
Pobierz#matematyka #algebra
Ktoś poleci jakiś dobry zbiór zadań do algebry? Kupiłem sobie "Wstęp do algebry 1" Kostrikina i fajnie by było, jak by by był jakiś kompatybilny.
Ktoś poleci jakiś dobry zbiór zadań do algebry? Kupiłem sobie "Wstęp do algebry 1" Kostrikina i fajnie by było, jak by by był jakiś kompatybilny.
@pococimojlogin: parę fajnych zadań od mojego byłego wykładowcy: http://home.agh.edu.pl/~gora/algebra/zestaw01.pdf numerki lecą do 12
- 1
@pococimojlogin: Nie wiem, czy najlepszy, ale na pewno bardzo dobry. Nie zmarnowałeś kasy.
#algebra #matematyka #studbaza #studbazaproblems
Czy mógłby mi ktoś podpowiedzieć, czego się uchwycić w tym dowodzie przez indukcyję?
To nie praca domowa, tylko wyczajone gdzieś w sieci zadania do poćwiczenia.
Czy mógłby mi ktoś podpowiedzieć, czego się uchwycić w tym dowodzie przez indukcyję?
To nie praca domowa, tylko wyczajone gdzieś w sieci zadania do poćwiczenia.

źródło: comment_0jj9QV2Uijhff58ZL8ae3flCaPW80eo0.jpg
Pobierz@gimbusiarz: teraz pewnie macie koła w gimbazie?
zadania do poćwiczenia
@OrestesGaolin: chyba ataków histerii :D
wypisz dane, wypisz szukane, rozpłacz się
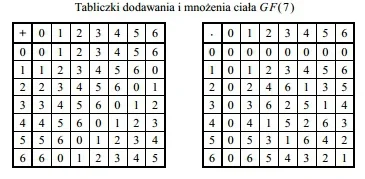
@Angel_of_death: poprawcie mnie jeśli się mylę, to jest dodawanie/mnożenie modulo, mod 7 chyba.
@Angel_of_death: To tak jak z zegarkiem, który ma 7 godzin.
13
Jak muzułmanie nie wynaleźli algebry
Kontynuując dyskusję na temat tego, co muzułmanie zrobili dla świata – lub raczej czego nie zrobili – musimy przyjrzeć się fałszywemu i dość rozpowszechnionemu przekonaniu, że wynaleźli oni algebrę.
z- 0
- #
- #
- #
- #
- #
- #
- #