#bitwyjezykowe
będziemy sobie je porównywać który lepszy
W lewym narożniku #visualbasic rozszerzenie leciwego Basica do Microsoftu
W prawym narożniku #wolfram Język stojący za sukcesem WolframAlpha
głosowanie plusami w kometarzach
Wszystko
Najnowsze
Archiwum
11

Pod Myszkowem zalega ponad 550 mln ton rud molibdenowo-wolframowych z miedzią. O tym, że to prawdopodobnie największe w Europie złoża wolframu znajdują się w okolicach tego miasta wiadomo od dawna. Inwestorzy są przekonani o sukcesie, samorządy protestują.
z4

Krótka relacja z wczorajszych ćwiczeń antyterrorystycznych na stacji metra Stare Bielany - w akcji Policja, Straż Pożarna, Pogotowie, a nawet śmigłowiec LPR. 00:15 - Rozpoczęcie ćwiczeń 00:37 - Przyjazd pierwszych służb 02:13 - Lądowanie śmigłowca LPR 04:28 - Przejazdy służb 04:35 - Przyjazd Unimoga
z
źródło: comment_1649407398krIUWt71brW4HaHESbeN0Y.jpg
Pobierz
źródło: comment_1649277550HY78IsCyIqaJ9s81UjJjgk.jpg
Pobierz
źródło: comment_1606038037eOb1t3YsRpNyI3DbuMFLn9.jpg
Pobierz4
Wystarczy przesłać zdjęcie i sztuczna inteligencja powie Ci co jest na tym obrazku.
z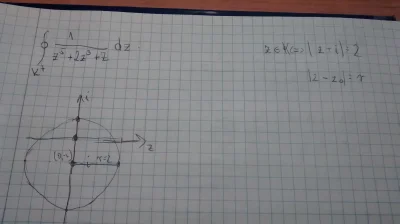
źródło: comment_bgoUeoVFUTvy9iiCLB0y4Ae1ZLOYBqyc.jpg
PobierzRegulamin
Reklama
Kontakt
O nas
FAQ
Osiągnięcia
Ranking
Jak ją wprowadzam do wolframowej matematyki, to zależnie od złożoności równania jest ok, albo zupełnie nie potrafi jej zinterpretować. Przykładem mogą być chociażby układy równań, które napisane w składni LaTeX'owej są
Z kolei dla układu równań, to już chyba nie jest tak fajnie. Wtedy polecenie solve 4x+2y=8, 5x+3y=9 załatwia sprawę, ale jednak musiałbyś robić ręcznie zmiany, czego zapewne chciałeś uniknąć