Treść przeznaczona dla osób powyżej 18 roku życia...

lizardking_21


Komentarz usunięty przez autora Wpisu
Komentarz usunięty przez autora Wpisu

źródło: comment_glwEX7Hf9iNqMd84nsOuw95BLdoY6JzD.jpg
Pobierz>ornstein i smough trudni

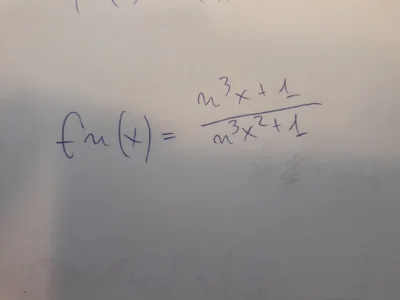
źródło: comment_o1uwhDnrT7z1WMfJvWOHnGRgMyB5lfW3.jpg
Pobierz
źródło: comment_zNXB1RAXUGqxWAzlYZsPrPPhB2XX8JOL.jpg
Pobierz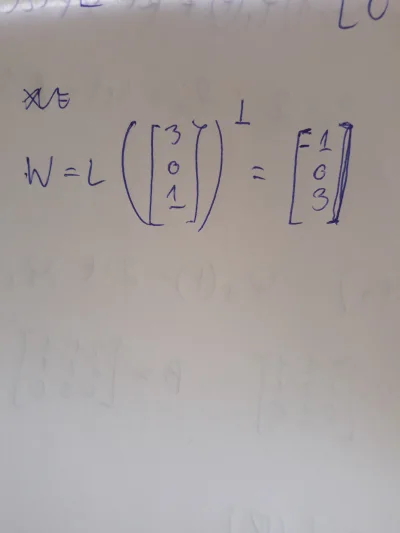
źródło: comment_rIIlVoqkE2pECrR9dz7tPEcnnr94lKE1.jpg
PobierzRocznica
od 10.03.2025
Gadżeciarz
od 19.01.2017
Mikroblogger
od 21.06.2016
Regulamin
Reklama
Kontakt
O nas
FAQ
Osiągnięcia
Ranking