Halo, ta herezja ma rację bytu? Jeśli tak to nk mi to wytłumaczy.
#matematyka
#matematyka
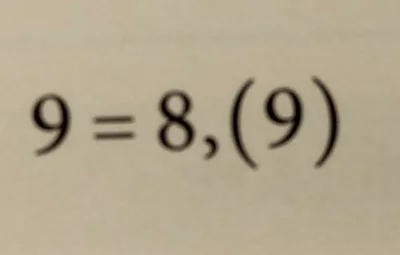
źródło: comment_Tg3qP9IU9t0DqyMbHkX5VErg3ia18lFO.jpg
Pobierza dowody są banalnie proste.
albo x=0,999999..../*10
10x=9,999999..../-x
the real number 0.999... is the set of rational numbers r such that r < 0, or r < 0.9, or r < 0.99
Generalnie
Czym twoim zdaniem są liczby rzeczywiste?
co pozwala na nieskończone mnożenie nie ma żadnego matematycznego sensu
ma ona tę wadę, że nie rozstrzyga o istnieniu takich liczb.
Pozwala na to definicja mnożenia w ciele R, która nakazuje nam mnożyć odpowiadające tym zapisom ciągi wyraz po wyrazie.
Dodam też może dla porządku, że szereg to ciąg sum częściowych, bo chyba coś ci się pozornie kłóci z tym co napisałem, mimo że
źródło: comment_atVQY6gVf08KozC6XM2RgxCSOC27hWxa.jpg
PobierzKtóry język programowania, będzie najszybszym do obliczeń matematycznych?
crysis nie mial multi

źródło: comment_WwtYhhBAO1uu2zexCDVitXm38OFXXvEw.jpg
Pobierz
źródło: comment_ocOf6tXfbGorUsAjGRYiKMz0E2oLjbb9.jpg
PobierzKomentator
od 10.01.2018
Rocznica
od 07.07.2025
Regulamin
Reklama
Kontakt
O nas
FAQ
Osiągnięcia
Ranking
źródło: https://ourworldindata.org/plastic-pollution
#mapporn #azja #ciekawostki
źródło: comment_J8A0880mba6AoMukWoRuLHWbyMl6dMu6.jpg
Pobierz@xeerxees: To nie jest prawda. Wcześniej był na przykład Singapur.
Co więcej, to wszystko wydaje się mieć jedną z przyczyn w tym, że kilka miesięcy temu (w okolicy naszych afer z podpaleniami wysypisk) Chiny zabroniły importowania śmieci plastikowych na swój teren, więc nagle się okazało, że nie ma co zrobić ze śmieciami.