Aktywne Wpisy

rales +257
tag do obserwowania --> #sredniasondazysejm
CZERWIEC 2023
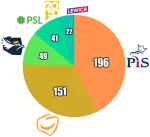
1. Prawo i Sprawiedliwość - 33,6% - 196 mandatów ( b.z)
2. Koalicja Obywatelska - 30,1% - 155 mandatów (⬆ 3,7%)
3. Konfederacja - 11,5% - 49 mandatów (⬆ 1,8%)
4. Trzecia Droga - 9,9% - 41 mandatów (⬇ 3%)
5. Lewica - 7,4% - 22 mandaty (⬇ 1,9%)
CZERWIEC 2023
1. Prawo i Sprawiedliwość - 33,6% - 196 mandatów ( b.z)
2. Koalicja Obywatelska - 30,1% - 155 mandatów (⬆ 3,7%)
3. Konfederacja - 11,5% - 49 mandatów (⬆ 1,8%)
4. Trzecia Droga - 9,9% - 41 mandatów (⬇ 3%)
5. Lewica - 7,4% - 22 mandaty (⬇ 1,9%)

Robił ktoś z Was mały ślub cywilny i obiad weselny tylko dla rodziców i rodzeństwa? Bez chrzestnych, ciotek i wujków, jak Wasi rodzice na to zareagowali? #slub #slubcywilny #wesele





Matemaks radzi, by pod pierwiastkiem znajdował się największy wyraz ciągu pierwszego pomnożony razy ilość wyrazów.
#matematyka #studbaza #polibuda
w sensie jak masz pierwiastek ntego stopnia to zazwyczaj to co pod pierwiastkiem najwieksze dla duzych n, to do tego dazy, to wskazowka i cisniesz tak zeby ograniczyc z dwoch stron podobnymi ciagami zbieznymi