spinacz61
  • 0
Czy ktoś z was kiedyś edytował słowa runiczne i dodawał jakieś nowe? Nabrałem się, że w starym diablo 2 LOD można zrobić insight w łuku, a się nie da. Jestem jednak zbyt podjadamy, żeby odpuścić xD Może ktoś pomoże? #diablo2
  • 2
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
ZdeformowanyKreciRyj
  • 2
@spinacz61:
1. żeby n(b_n - b_{n-1}) rozbiegało to od pewnego miejsca musi być b_n - b_{n-1} > 1/n
2. b_n musi spełniać warunek cauchyego
3. dla m > n możemy zapisać b_m - b_n = \sum_{i = n+1}^{m} b_i - b_{i-1} ale z punktu 1 wiemy, że od pewnego n każdy wyraz sumy musiałby być większy od 1/n a taki szereg jest rozbieżny skąd jest sprzeczność z tym, że b_n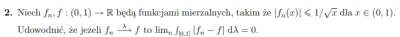
  • Odpowiedz
Krolowa_Nauk
  • 0
@spinacz61: możemy zrobić kółko wspólnego rozkminiania zadań. Na przykład ostatnio zastanawiałam się jak pokroić prostokątną pizzę na trzy równe części tak, żeby każda miała tyle samo brzegu. Zadanie proste, już zrobione, ale ciekawe konkluzje mi wyszły, bo przy specyficznych założeniach sposobu krojenia wychodziły mi specyficzne stosunki boków całego prostokąta, jakie muszą być spełnione, żeby się to udało. Także możemy się umówić, że jak ktoś wpadnie na jakieś zagadnienie, to tutaj
  • Odpowiedz
Blomex
Blomex
Blomex
via Wykop Mobilny (Android)
  • 0
X - przyjmuje wartości -1, 1 z prawd 1/4 (tylko gdy Y przyjmuje wartość 1) oraz wartość 0, gdy Y przyjmuje wartość 3.
Y - przyjmuje wartość 3 z prawd. 50% i wartość 1 z prawd 50%.

Takie coś nie zadziała? Nie są niezależne, to chyba widać.
  • Odpowiedz
spinacz61
  • 9
Napiszę ten wysryw, bo niemiłosiernie śmieszy mnie dzisiejsza młodzież i jej podejście do matmy.

tl;dr
Ludzie przychodzą na korki za późno (z naprawdę ogromnymi brakami), marnują pieniądze opiekunów albo chodzą na marne, bo boją się przyznać, że czegoś nie rozumieją.

Prowadzę korki z matmy dla podstaówkowiczów i średniaków. Braki wiedzy wśród ludzi są przeróżne. Są dzieci, a raczej nastolatkowie, w 7 czy 8 klasie podstawówki, które mają problemy z działaniami na liczbach, a raz nawet
  • 16
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
dziwna_kuna
  • 3
@spinacz61: Z jednej strony trochę Cię rozumiem a z drugiej strony trochę przesadzasz. Niektórzy uczniowie po prostu nie wiedzą jak wygląda normalna nauka, nie potrafią zadawać pytań albo się po prostu tego boją bo np. mają wredną nauczycielkę. Uczyłem wiele osób i rzadko się zdarzało że komuś coś wytłumaczyłem on powiedział że to rozumie a potem nie wiedział co robić (pewnie dlatego że zwykle sam sprawdzam czy potrafi rozwiązać podobny
  • Odpowiedz
spinacz61
  • 0
Ma ktoś coś fajnego na temat funkcji analitycznych? Jakoś nie kupuje mnie to całkowanie po krzywych, holomorficzność itp. O ideach rozszerzenia ciała R do ciała C też możecie coś podrzucić

#matematyka
  • 2
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
tomekgz
tomekgz
  • 1
@spinacz61:
Chądzyński - Wstęp do analizy zespolonej.
Chądzyński - Wstęp do analizy zespolonej w zadaniach.
Żakowski, Leksiński - z serii EiT, IV tom.
  • Odpowiedz
spinacz61
  • 0
Moim pomysłem jest to, że ze zbieżności według miary, dla dostatecznie dużych n zachodzi |fn - f| < epsilon na zbiorze prawie całej miary, co można oszacować przez całkę po całym (0,1) z epsilon.

Ale ta druga część, gdzie ten moduł jest większy niż epsilon sprawia mi problem. Co prawda jest to zbiór dowolnie małej miary, ale nie wiadomo, jak się zachowuje ta funkcja. I tutaj powinno wejść założenie, że |f
spinacz61 - Moim pomysłem jest to, że ze zbieżności według miary, dla dostatecznie du...

źródło: comment_1643927298ntztJZwJwRVZPLUECay5lV.jpg

Pobierz
  • 3
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
tyrytyty
  • 2
@spinacz61: dla dowolnego podciągu f(n) istnieje podciąg taki (jaki konkretnie?), że można do niego zastosować tw. Lebesgue'a o zbieżności zmajoryzowanej z g = 1/sqrt(x).

jeśli każdy podciąg ciągu ma podciąg zbieżny, to cały ciąg jest zbieżny
  • Odpowiedz
spinacz61
  • 2
Pierwsza całka, lecę na zdominowanego Lebesgue'a, szacuję z góry i dostaję takie oszacowanie. Mój pomysł to rozbicie zbioru na (-inf, -1) u (1, inf) i szacowanie przez 1/x^2 na tym zbiorze, a na [-1,1] szacowanie przez x^2+1 albo nawet przez stałą = 2. Czy jest jakiś inny sposób aby pokazać, że funkcja g jest całkowalna na R?
#matematyka
spinacz61 - Pierwsza całka, lecę na zdominowanego Lebesgue'a, szacuję z góry i dostaj...

źródło: comment_1643715742X00wqmarTomuTSyAu9nZ1S.jpg

Pobierz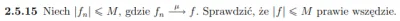
  • 6
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
spinacz61
  • 0
Jakiś pomysł na to zadanie? Doszedłem do wniosku, że te zbiory nie mogą być parami rozłączne, ale nie widzę, do czego to może być przydatne. Dodatkowo gdyby rozbić ten zbiór domknięty na zbiór otwarty suma końce, to wystarczyłoby pokazać, że końców jest przeliczalnie wiele, więc już wszystko by było. Oczywiście chodzi o nieprzeliczalny przypadek
#matematyka
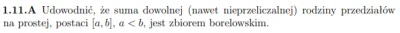
spinacz61 - Jakiś pomysł na to zadanie? Doszedłem do wniosku, że te zbiory nie mogą b...

źródło: comment_1636124483VZ2fdMyPY20IiwWdENW2RV.jpg

Pobierz
  • 7
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
Krolowa_Nauk
  • 3
@tyrytyty: coś w tym jest, chociaż ja bym przedefiniowała słowo "debil", bo mam wrażenie, że to nie jest tak, że jak ktoś wrzuci rozwiązanie zadania przede mną, albo nawet rozwiązanie zadania, na które bym nie wpadła, to od razu czyni ze mnie "debila".
Zawsze w każdej dziedzinie znajdziesz kogoś lepszego i gorszego od siebie. Fakt, że napisało się rozszerzoną maturę z matematyki sprawia, że (według pewnej miary) jest się lepszym
  • Odpowiedz
tyrytyty
  • 1
@spinacz61: jak L1=L2=L3 to 3L1 + 5L2 - 7L3 = L1, więc byłoby łatwo wtedy.

v1 = 2v2 - v3, to wektory własne więc nakładając A

L1 v1 = L1 (2v2 - v3) = 2L2 v2 - L3 v3 (środkowe przez to że =v1, prawe nakładając A
  • Odpowiedz
spinacz61
  • 0
Mirki, bo nie mogę się przekonać do tej myśli. Mamy zbiór wszystkich funkcji z X w Y ozn. Y^X. Ustalmy B zawarte w Y. Czy wtedy B^X jest podzbiorem Y^X? Według mnie tak, chociaż nie jestem jakoś super pewny tego.

Ustalmy dow. f należące do B^X. To oznacza, że f jest funkcją z X w B, czyli mamy, że f zawiera się w X x B. Z zawierania B w Y mamy,
  • 11
  • Odpowiedz

  • Otrzymuj powiadomienia
    o nowych komentarzach
k.....e
  • 2
@spinacz61: bo aż sam się musiałem zastanowić xD

generalnie Twoje rozumowanie jest dobre - jeśli (zmieniam literki bo pisanie Xx jest debilne) B jest podzbiorem Y, to AxB jest podzbiorem AxY, więc funkcja zawierająca się w AxB będzie się też zawierała w AxY.

ogólnie zasada jest taka, i zakładam że tu jest niejasność, że przy definiowaniu funkcji zawsze potrzebne są trzy rzeczy: dziedzina, przedziwdziedzina i wzór (czy ogólnie, opis przekształcenia
  • Odpowiedz

Osiągnięcia