Aktywne Wpisy

SebastianDosiadlgo +199
#zalesie Dzieci w podstawówce lat 9+ sikały ze szczęścia jak zobaczyły w zamrażarce sklepowej lody Ekipy od Friza i wymieniały się na przerwach papierkami po lodach.
Tępe NPC-e lat 18+ sikają ze szczęścia, że mogą wypić przesłodzoną wodę w super-cool-hype-trendy żółtej puszce za 6.99 zł a potem jeszcze pójdą do kina, żeby obejrzeć kiczowaty film-laurkę o typie z instagrama, który zarobił na takich idiotach kilkanaście milionów xD xD
Nie wiem kto jest
Tępe NPC-e lat 18+ sikają ze szczęścia, że mogą wypić przesłodzoną wodę w super-cool-hype-trendy żółtej puszce za 6.99 zł a potem jeszcze pójdą do kina, żeby obejrzeć kiczowaty film-laurkę o typie z instagrama, który zarobił na takich idiotach kilkanaście milionów xD xD
Nie wiem kto jest
źródło: 41b5aa269d974241a951b2791a97b2202056422ce0ebec786ffde3301de14a06
Pobierz
xiv7 +5





#matematyka #ciekawostki #popularnonaukowe #gruparatowaniapoziomu
(Poprzedni wpis o teorii mocy i różnych nieskończonościach)
Wiecie co matematycy lubią robić najbardziej? Uogólniać znane koncepty. Nie powinno więc dziwić, że znane wszystkim struktury algebraiczne, czyli zbiory wyposażone w działania (np. liczby całkowite z dodawaniem) rozpatrywane były w bardziej ogólny sposób, przyglądając się jakie własności zachodzą dla tych dobrze znanych obiektów. Tak powstał dział zajmujący się różnymi strukturami algebraicznymi, zwany algebrą abstrakcyjną.
Strukturą algebraiczną nazywamy zbiór wyposażony w działania na nim. Rozpatrywać będziemy tylko działania binarne, czyli funkcje ∘: A×A→ A (bierzemy dwa elementy zbioru i zwracamy jakiś inny element będący wynikiem). Najprostszym przykładem jest zbiór wyposażony w jedno działanie: (A, ∘). Taką strukturę nazywamy:
- półgrupą, jeśli działanie ∘ jest łączne, to znaczy dla dowolnych elementów x, y, z zbioru A zachodzi: x ∘ (y ∘ z) = (x ∘ y) ∘ z. Dzięki tej własności można zapisywać po prostu x ∘ y ∘ z i nie przejmować się nawiasami, bo to jak pogrupujemy czynniki wyrażenia nie ma znaczenia.
- monoidem, jeśli jest to półgrupa z wyróżnionym elementem neutralnym e, takim, że dla każdego x zachodzi x ∘ e = e ∘ x = x. [a monada to podobno monoid w kategorii endofunktorów ͡° ͜ʖ ͡°)]
Dosyć znanym przykładem struktury algebraicznej (z dwoma zbiorami i dwoma działaniami) jest przestrzeń wektorowa, o której pisałem wcześniej ( ͡° ͜ʖ ͡°)
Tyle z ogólnych informacji, czas zdefiniować czym są te słynne grupy. Otóż grupą nazywamy zbiór wyposażony w jedno działanie binarne (G, ∘) o następujących własnościach:
- działanie ∘ jest łączne
- istnieje element neutralny e (wiemy więc już, że grupa jest monoidem)
- dla każdego elementu grupy, istnieje element odwrotny względem działania ∘, czyli dla każdego x istnieje y takie, że x ∘ y = e.
Jak się trochę zastanowimy, to dojdziemy do wniosku, że wiele znanych nam algebr spełnia wszystkie te wymagania. Grupami są na przykład: zbiór liczb całkowitych z dodawaniem (Z, +), zbiór liczb rzeczywistych bez zera z mnożeniem (R \ {0}, ∙), liczby wymierne z dodawaniem (Q, +). Grupą za to NIE JEST zbiór liczb całkowitych z mnożeniem, ponieważ brakuje tam odwrotności (np. nie ma takiej liczby całkowitej x, że 2x = 1). Z tego samego powodu przykładem nie mogą być liczby naturalne z działaniem dodawania.
Z przykładów widać, że definicja nie jest pozbawiona sensu i rzeczywiście uogólnia znane wcześniej struktury, ale co z tego? Jakie są mniej oczywiste przykłady grup? A, dobrze, że pytasz! Różne, rozmaite, rzec można. Kultowym przykładem, który zawsze musi paść, jest zbiór działań możliwych do wykonania na kostce Rubika. Obroty ścianek możemy łączyć, każdy obrót można cofnąć i jest element neutralny, polegający na nie robieniu nic - wszystko się zgadza.
Innymi przykładami mogą być różne grupy macierzowe z działaniem mnożenia, takie jak:
- GL(R, N) - odwracalne macierze NxN liczb rzeczywistych
- SL(R, N) - odwracalne macierze NxN liczb rzeczywistych, których wyznacznik równy jest 1
- SO(R, N) - zbiór ortogonalnych macierzy NxN (takich, że AA^T = I)
- SU(N) - zbiór macierzy unitarnych
Grupy macierzowe są ciekawe same w sobie, ze względu na to, że są to grupy Lie, istotne w robotyce czy fizyce (kwantowa teoria pola). SL(2, Z) pojawia się zaś przy formach modularnych.
Szeroką grupę (hehe) grup tworzą zbiory liczb {0, 1, 2, ..., n-1} z działaniem dodawania modulo n (to znaczy, że dodajemy liczby tak jak godziny na zegarze: 11 + 2 = 1 bo po 12 wracamy do 1; analogicznie jest przy dodawaniu modulo n, tylko że wracamy do 0 po dojściu do n). Takie grupy oznacza się jako Zn albo Z/nZ. Na przykład Z4 to grupa o czterech elementach. Często przedstawia się strukturę algebr za pomocą tablicy Cayleya, czyli takiej "tabliczki mnożenia", gdzie działaniem niekoniecznie jest mnożenie. Dla naszego przykładu wygląda ona tak:
+ 0 1 2 30 0 1 2 3
1 1 2 3 0
2 2 3 0 1
3 3 0 1 2
Możemy zauważyć, że powyższa tabelka jest symetryczna. To znaczy, że dla dowolnych elementów grupy x+y = y+x. Tak nie musi być zawsze. Jeśli jednak tak jest, to grupę nazywamy przemienną lub abelową (abelian po angielsku; od nazwiska matematyka - Niels Henrik Abel). Wszystkie grupy Zn są przemienne, co dosyć oczywiste. GL(R, N) nie jest przemienne.
Czas na kilka definicji, a potem kolejne przykłady. Rząd grupy G to liczba jej elementów. Oznacza się |G|, ord(G) albo r(G).
Podgrupą grupy (G, ∘) nazywamy podzbiór S ⊆ G z działaniem ∘ ograniczonym na zbiór S, jeśli (S, ∘) tworzy grupę. Kłopot polega na tym, że biorąc dowolne dwa elementy losowego pozbioru i wykonując na nim działanie grupy możemy otrzymać element nienależący do podzbioru. Szukanie podgrup niekoniecznie jest więc proste. Przykładem podgrupy może być ({-1, 1}, ∙) względem grupy (R \ {0}, ∙). Poszukiwania podgrup może ułatwić nam twierdzenie Lagrange'a, które mówi, że jeśli G jest grupą skończoną i H jest podgrupą, to ord(H)|ord(G) czyli rząd podgrupy dzieli rząd całej grupy. Wnioskiem z tego twierdzenia jest to, ze grupy, których liczba elementów jest liczbą pierwszą mogą mieć jedynie podgrupę trywialną, czyli składającą się jedynie z elementu neutralnego, albo podgrupą jest cała grupa. Grupa 8-elementowa może (ale nie musi) mieć podgrupy o rozmiarach 1, 2, 4, 8 - podgrup o innych rozmiarach nie ma sensu szukać.
Kiedy rozmawiamy ogólnie o grupach, często wygodnie jest przyjąć notację multiplikatywną. W takiej notacji wyobrażamy sobie, że działanie grupy ∘ działa jak mnożenie. Wtedy r^2 oznacza r∘r, r^0 = e, a r^-1 jest elementem odwrotnym, czyli r ∘ r^-1 = e. Istnieje również analogiczna notacja addytywna, wtedy 2r = r∘r, bo wyobrażamy sobie, że ∘ to dodawanie.
Podgrupę generowaną przez jeden element r, nazywamy zbiór <r> = {r^k : k ∊ Z} (notacja multiplikatywna). Na przykład dla (Z, +) <2> = {0, 2, -2, 4, -4, ...}, albo dla Z6 <3> = {0, 3}.
Rząd elementu to rozmiar podgrupy, którą generuje. Jeśli element r generuje całą grupę, to znaczy <r> = G, to wtedy r nazywamy generatorem grupy. Grupy mające generator nazywamy cyklicznymi. Wszystkie grupy Zn są cykliczne, ponieważ generuje je 1.
Niektóre grupy nie są generowane przez jeden element, ale wciąż można stworzyć każdy element grupy za pomocą skończonej liczb jej elementów. Wtedy zbiór tych elementów nazywa się generatorami.
Czas na kolejny, bardziej geometryczny, przykład grup. Grupy diedralne (albo dihedralne? nie umiem metematyki po polsku...) to grupy symetrii n-kąta foremnego z działaniem kompozycji, oznaczane Dn (albo D2n... zależy czy zapisujemy liczbę elementów czy ile kątów ma figura, którą grupa opisuje). Dla przykładu, grupa D4 opisuje symetrie kwadratu. Jej elementami są: e - element neutralny, który nie robi nic, r - obrót o 90 stopni w prawo, r^2, obrót o 180 stopni, r^3 - obrót o 270 stopni, s - odbicie lustrzane w jednej z osi i tak dalej. W ramach ćwiczenia możesz spróbować znaleźć wszystkie elementy tej grupy i zapisać tablicę Cayleya. Powinieneś znaleźć 8 elementów. Poniżej przykład działania elementu s:
A +-------+ B B +-------+ A| | s | |
| | ----> | |
| | | |
C +-------+ D D +-------+ C
Okazuje się, że grupa D4 jest generowana przez obrót o 90 stopni oraz odbicie - dowolną symetrię kwadratu można uzyskać łącząc ze sobą te dwie operacje. Na przykład, odbicie w osi X:
A +-------+ B C +-------+ D| | s_x | |
| | ----> | |
| | | |
C +-------+ D A +-------+ B
można zrealizować obracając kwadrat dwukrotnie, a potem odbijając go w osi Y:
A +-------+ B C +-------+ A D +-------+ C C +-------+ D| | r | | r | | s | |
| | ----> | | ----> | | ----> | |
| | | | | | | |
C +-------+ D D +-------+ B B +-------+ A A +-------+ B
innymi słowy sx = r^2s.
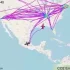
Ciekawym sposobem wizualizacji grup jest diagram/graf Cayleya, w którym generatory widoczne są jako krawędzie o różnych kolorach, a elementami są węzły. Przykład diagramu dla grupy D4 jest dołączonym obrazie (z angielskiej wikipedii).
Kompaktowym zapisem grupy jest prezentacja grupy, na którą składa się zbiór generatorów i relacje zachodzące między nimi. Na przykład dla dowolnej grupy Dn zachodzą własności: r^n = e, s^2 = e oraz sr = rs^(n-1). Z tego powodu (jedna z możliwych) prezentacja grupy Dn jest następująca: Dn = <r, s | r^n = e, s^2 = e, sr = rs^(n-1)>. Mając te informacje możemy wykonać dowolne działanie w grupie.
To by było na tyle jeśli chodzi o ten wpis. O grupach można by powiedzieć wiele więcej. Być może w następnym wpisie będzie o grupach ilorazowych i homomorfizmach, albo od razu o pierścieniach. W każdym razie na pewno nie będzie o twierdzeniach o izomorfizmie, tw. Sylowa, klasyfikacji grup skończonych, klasyfikacji grup prostych, grupach sporadycznych.
źródło: Dih_4_Cayley_Graph;_generators_a,_b.svg
Pobierz@mecenasie: Inny, żart z tematu:
Diabeł dał inżynierowi, fizykowi i matematykowi siatkę ogrodzeniową o takiej samej długości i kazał nią ogrodzić jak największą przestrzeń.
Inżynier: zrobił z niej zgrabny kwadrat,
fizyk: patrzą z pogardą na inżyniera, zrobił okrąg,
matematyk: rozstawił byle jak, wszedł do środka i powiedział że jest na zewnątrz.
źródło: Alutka_F
PobierzKomentarz usunięty przez autora
źródło: comment_MYNSZR8BpyciRKt5iG1oYDSPNPg5soSA
PobierzKomentarz usunięty przez autora
PS. Za post plusik.
źródło: temp_file5973157332452063480
Pobierz@important_sample: Liego :). U mnie na studiach odmieniali Norwega :)
Umiesz tłumaczyć. Pisz więcej.